| Communications Toolbox | |
Representing Block Coding Parameters
This subsection describes the items that you might need in order to process [n,k] linear block codes. The table below lists the items and the coding techniques for which they are most relevant.
| Parameter |
Block Coding Technique |
| Generator Matrix |
Generic linear block |
| Parity-Check Matrix |
Generic linear block |
| Generator Polynomial |
Cyclic, BCH, Reed-Solomon |
| Primitive Polynomial and List of Galois Field Elements |
Hamming, Reed-Solomon |
| Decoding Table |
Generic linear block, Hamming |
Generator Matrix
The process of encoding a message into an [n,k] linear block code is determined by a k-by-n generator matrix G. Specifically, the 1-by-k message vector v is encoded into the 1-by-n codeword vector vG. If G has the form [Ik P] or [P Ik], where P is some k-by-(n-k) matrix and Ik is the k-by-k identity matrix, then G is said to be in standard form. (Some authors, e.g., Clark and Cain [1], use the first standard form, while others, e.g., Lin and Costello [2], use the second.) Most functions in this toolbox assume that a generator matrix is in standard form when you use it as an input argument.
Some examples of generator matrices are in the next section, Parity-Check Matrix.
Parity-Check Matrix
Decoding an [n,k] linear block code requires an (n-k)-by-n parity-check matrix H. It satisfies GHtr = 0 (mod 2), where Htr denotes the matrix transpose of H, G is the code's generator matrix, and this zero matrix is k-by-(n-k). If G = [Ik P] then H = [-Ptr In-k]. Most functions in this toolbox assume that a parity-check matrix is in standard form when you use it as an input argument.
The table below summarizes the standard forms of the generator and parity-check matrices for an [n,k] binary linear block code.
| Type of Matrix |
Standard Form |
Dimensions |
| Generator |
[Ik P] or [P Ik] |
k-by-n |
| Parity-check |
[-P' In-k] or [In-k -P' ] |
(n-k)-by-n |
Ik is the identity matrix of size k and the ' symbol indicates matrix transpose. (For binary codes, the minus signs in the parity-check form listed above are irrelevant; that is, -1 = 1 in the binary field.)
Examples. In the command below, parmat is a parity-check matrix and genmat is a generator matrix for a Hamming code in which [n,k] = [23-1, n-3] = [7,4]. Notice that genmat has the standard form [P Ik].
[parmat,genmat] = hammgen(3)
parmat =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
genmat =
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
The next example finds parity-check and generator matrices for a [7,3] cyclic code. The cyclpoly function is mentioned below in Generator Polynomial.
genpoly = cyclpoly(7,3);
[parmat,genmat] = cyclgen(7,genpoly)
parmat =
1 0 0 0 1 1 0
0 1 0 0 0 1 1
0 0 1 0 1 1 1
0 0 0 1 1 0 1
genmat =
1 0 1 1 1 0 0
1 1 1 0 0 1 0
0 1 1 1 0 0 1
The example below converts a generator matrix for a [5,3] linear block code into the corresponding parity-check matrix.
genmat = [1 0 0 1 0; 0 1 0 1 1; 0 0 1 0 1];
parmat = gen2par(genmat)
parmat =
1 1 0 1 0
0 1 1 0 1
The same function gen2par can also convert a parity-check matrix into a generator matrix.
Generator Polynomial
Cyclic codes, including the special cases of BCH and Reed-Solomon codes, have special algebraic properties that allow a polynomial to determine the coding process completely. This so-called generator polynomial is a degree-(n-k) divisor of the polynomial xn-1. Van Lint [4] explains how a generator polynomial determines a cyclic code.
The functions in this toolbox that produce generator polynomials are bchpoly, cyclpoly, and rspoly. They represent a generator polynomial using a row vector that lists the polynomial's coefficients in order of ascending powers of the variable. Functions dealing with BCH and generic cyclic codes use binary digits as coefficients, as in the first example below. Functions dealing with Reed-Solomon codes express the coefficients (which are elements of GF(2m)) in exponential format, as in the second example below. See Representing Elements of Galois Fields for a description of this exponential format for elements of Galois fields.
genpoly = cyclpoly(7,3)
genpoly =
1 0 1 1 1
finds that one valid generator polynomial for a [7,3] cyclic code is 1 + x2 + x3 + x4.
A second example finds that a generator polynomial for a [15,13] Reed-Solomon code is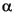 
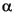3 + 5x + 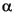0x2, where 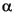is a root of MATLAB's default primitive polynomial for GF(15+1).
r = rspoly(15,13)
r =
3 5 0
Primitive Polynomial and List of Galois Field Elements
Hamming and Reed-Solomon codes rely on algebraic fields that have 2m elements (or, more generally, pm elements for a prime number p). Elements of such fields are named relative to a distinguished element of the field that is called a primitive element. Some functions in this toolbox use a primitive polynomial or a list of elements in the field as a way to determine the primitive element and, consequently, as a way to name elements of the field. See Galois Field Computations and especially the subsection Representing Elements of Galois Fields for details about MATLAB's use of primitive polynomials and lists of Galois field elements.
To reduce the mathematical background that you need to use the block coding functions, simply use the default parameters in commands that ask for primitive polynomials or lists of Galois field elements. For more specifics, see the reference pages for encode, decode, hammgen, rsenco, rsencode, rsdeco, rsdecode, and rspoly.
Decoding Table
A decoding table tells a decoder how to correct errors that may have corrupted the code during transmission. Hamming codes can correct any single-symbol error in any codeword. Other codes can correct, or partially correct, errors that corrupt more than one symbol in a given codeword.
This toolbox represents a decoding table as a matrix with n columns and 2n-k rows. Each row gives a correction vector for one received codeword vector. A Hamming decoding table has n+1 rows. The syndtable function generates a decoding table for a given parity-check matrix.
Example: Using a Decoding Table
The script below shows how to use a Hamming decoding table to correct an error in a received message. The hammgen function produces the parity-check matrix, while the syndtable function produces the decoding table. The transpose of the parity-check matrix is multiplied on the left by the received codeword, yielding the syndrome. The decoding table helps determine the correction vector. The corrected codeword is the sum (modulo 2) of the correction vector and the received codeword.
% Use a [7,4] Hamming code.
m = 3; n = 2^m-1; k = n-m;
parmat = hammgen(m); % Produce parity-check matrix.
trt = syndtable(parmat); % Produce decoding table.
recd = [1 0 0 1 1 1 1] % Suppose this is the received vector.
syndrome = rem(recd * parmat',2);
syndrome_de = bi2de(syndrome,'left-msb'); % Convert to decimal.
disp(['Syndrome = ',num2str(syndrome_de),...
' (decimal), ',num2str(syndrome),' (binary)'])
corrvect = trt(1+syndrome_de,:) % Correction vector
% Now compute the corrected codeword.
correctedcode = rem(corrvect+recd,2)
recd =
1 0 0 1 1 1 1
Syndrome = 3 (decimal), 0 1 1 (binary)
corrvect =
0 0 0 0 1 0 0
correctedcode =
1 0 0 1 0 1 1
| | Representing Messages and Codewords | Creating and Decoding Block Codes | |