

| Communications Toolbox |   |
Creating and Decoding Block Codes
The functions for encoding and decoding linear block codes are encode, decode, bchenco, bchdeco, rsenco, rsdeco, rsencode, rsdecode, rsencof, and rsdecof. The first two in this list are general-purpose functions that invoke other functions from the list when appropriate. This section discusses how to use these functions to create and decode generic linear block codes, cyclic codes, BCH codes, Hamming codes, and Reed-Solomon codes.
Generic Linear Block Codes
Encoding a message using a generic linear block code requires a generator matrix. If you have defined variables msg, n, k, and genmat, then either of the commands
code = encode(msg,n,k,'linear',genmat); code = encode(msg,n,k,'linear/decimal',genmat);
encodes the information in msg using the [n,k] code that the generator matrix genmat determines. The /decimal option, suitable when 2n and 2k are not very large, indicates that msg contains nonnegative decimal integers rather than their binary representations. See Representing Messages and Codewords or the reference page for encode for a description of the formats of msg and code.
Decoding the code requires the generator matrix and possibly a decoding table. If you have defined variables code, n, k, genmat, and possibly also trt, then the commands
newmsg = decode(code,n,k,'linear',genmat); newmsg = decode(code,n,k,'linear/decimal',genmat); newmsg = decode(code,n,k,'linear',genmat,trt); newmsg = decode(code,n,k,'linear/decimal',genmat,trt);
decode the information in code, using the [n,k] code that the generator matrix genmat determines. decode also corrects errors according to instructions in the decoding table that trt represents.
Example: Generic Linear Block Coding. The example below encodes a message, artificially adds some noise, decodes the noisy code, and keeps track of errors that the decoder detects along the way. Since the decoding table contains only zeros, the decoder does not correct any errors.
n = 4; k = 2; genmat = [[1 1; 1 0], eye(2)]; % Generator matrix msg = [0 1; 0 0; 1 0]; % Three messages, two bits each % Create three codewords, four bits each. code = encode(msg,n,k,'linear',genmat); noisycode = rem(code + randerr(3,4,[0 1;.7 .3]),2); % Add noise. trt = zeros(2^(n-k),n); % No correction of errors % Decode, keeping track of all detected errors. [newmsg,err] = decode(noisycode,n,k,'linear',genmat,trt); err_words = find(err~=0) % Find out which words had errors.
The output indicates that errors occurred in the first and second words. Your results might vary since this example uses random numbers as errors.
err_words =
1
2
Cyclic Codes
Encoding a message using a cyclic code requires a generator polynomial. If you have defined variables msg, n, k, and genpoly, then either of the commands
code = encode(msg,n,k,'cyclic',genpoly); code = encode(msg,n,k,'cyclic/decimal',genpoly);
encodes the information in msg using the [n,k] code determined by the generator polynomial genpoly. genpoly is an optional argument for encode. The default generator polynomial is cyclpoly(n,k). The /decimal option, suitable when 2n and 2k are not very large, indicates that msg contains nonnegative decimal integers rather than their binary representations. See Representing Messages and Codewords or the reference page for encode for a description of the formats of msg and code.
Decoding the code requires the generator polynomial and possibly a decoding table. If you have defined variables code, n, k, genpoly, and trt, then the commands
newmsg = decode(code,n,k,'cyclic',genpoly); newmsg = decode(code,n,k,'cyclic/decimal',genpoly); newmsg = decode(code,n,k,'cyclic',genpoly,trt); newmsg = decode(code,n,k,'cyclic/decimal',genpoly,trt);
decode the information in code, using the [n,k] code that the generator matrix genmat determines. decode also corrects errors according to instructions in the decoding table that trt represents. genpoly is an optional argument in the first two syntaxes above. The default generator polynomial is cyclpoly(n,k).
There are no lower-level functions that provide alternative means to process cyclic codes.
Example. The example in the section Generic Linear Block Codes can be modified so that it uses the cyclic coding technique, instead of the linear block code with the generator matrix genmat. Make the changes listed below:
genpoly = [1 0 1]; % generator poly is 1 + x^2
encode and decode commands), replace genmat by genpoly and replace 'linear' by 'cyclic'.Another example of encoding and decoding a cyclic code is on the reference page for encode.
BCH Codes
BCH codes are a special case of cyclic codes, though the decoding algorithm for BCH codes is more complicated than that for generic cyclic codes. The discussion in the section Cyclic Codes above applies almost exactly to the case of BCH codes. The only differences are that:
bch replaces cyclic in the syntax for encode and decode.bchpoly(n,k) replaces cyclpoly(n,k) as the default generator polynomial.n and k must be valid codeword and message lengths for BCH code.Valid codeword lengths for BCH code are those integers of the form 2m-1 for some integer m greater than or equal to 3. Given a valid BCH codeword length, the corresponding valid BCH message lengths are those numbers in the second column of the output of the command below.
params = bchpoly(n); % Where n = 2^m-1 for some integer m >= 3
For example, the output of the command below shows that a BCH code with codeword length 15 may have message length 5, 7, or 11. No other message lengths are valid for this codeword length.
params = bchpoly(15)
params =
15 11 1
15 7 2
15 5 3
The third column of the output above represents the error-correction capability for each pair of codeword length and message length.
Choice of Functions for BCH Coding. To process BCH codes, you can use either the encode and decode functions, or the lower-level bchenco and bchdeco functions. The syntax of the lower-level functions is slightly different from that of the higher-level functions. The only difference in functionality is that the higher-level functions prepare the input data (including default values of options that you omit) before invoking the lower-level commands. The reference page for encode contains an example that uses encode and decode. The reference pages for bchenco and bchdeco contain other examples.
Hamming Codes
The reference pages for encode and decode contain examples of encoding and decoding Hamming codes. Also, the section Decoding Table illustrates error-correction in a Hamming code. There are no lower-level functions that provide alternative means to process Hamming codes.
Reed-Solomon Codes
Reed-Solomon codes are useful for correcting errors that occur in bursts. The codeword length n of a Reed-Solomon code must have the form 2m-1, where m is an integer greater than or equal to 3. The error correction capability of a Reed-Solomon code is floor((n-k)/2). Since n is an odd number, the coding is more efficient when the message length k is also odd.
One difference between Reed-Solomon codes and the other codes supported in this toolbox is that Reed-Solomon codes process symbols in GF(2m) instead of GF(2). Each such symbol is specified by m bits. That is why some parts of the section Representing Messages and Codewords make exceptions for Reed-Solomon codes.
Encoding a message using a Reed-Solomon code requires a generator polynomial. The rspoly function finds generator polynomials. For example, the command
genpoly = rspoly(15,12)
genpoly =
6 13 11 0
shows that the generator polynomial for a [15,12] Reed-Solomon code is
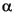 6 +
6 + 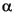 13x +
13x + 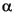 11x2 + x3
11x2 + x3
where 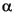 is a root of MATLAB's default primitive polynomial for GF(16). In this example, m = 4,
is a root of MATLAB's default primitive polynomial for GF(16). In this example, m = 4, n = 2m-1 = 15, and k = 12.
Choice of Functions for Reed-Solomon Coding. To process Reed-Solomon codes, you can use either the encode and decode functions, or the lower-level rsenco, rsdeco, rsencode, and rsdecode functions. The syntax of the lower-level functions is slightly different from that of the higher-level functions. The only difference in functionality is that the higher-level functions prepare the input data (including default values of options that you omit) before invoking the lower-level functions. The reference pages for the lower-level functions contain examples that illustrate their use.
 | Representing Block Coding Parameters | Performing Other Block Code Tasks |  |