Communications Toolbox

Representing Elements of Galois Fields

This section discusses how to represent Galois field elements using this toolbox's exponential format and polynomial format. It also describes a way to list all elements of the Galois field, because some functions use such a list as an input argument. Finally, it discusses the nonuniqueness of representations of Galois field elements.

The elements of GF(p) can be represented using the integers from 0 to p-1.

When m is at least two, GF(p^m) is called an extension field. Integers alone cannot represent the elements of GF(p^m) in a straightforward way. MATLAB uses two main conventions for representing elements of GF(p^m): the exponential format and the polynomial format.

Note    Both the exponential format and the polynomial format are relative to your choice of a particular primitive element of GF(pm).

Exponential Format

This format uses the property that every nonzero element of GF(p^m) can be expressed as ^c for some integer c between 0 and p^m-2. Higher exponents are not needed, since the theory of Galois fields implies that every nonzero element of GF(p^m) satisfies the equation x^q-1 = 1 where q = p^m.

MATLAB's use of the exponential format is shown in the table below.

Table 2-10: Exponential Format in MATLAB 

Element of GF(pm)	MATLAB Representation of the Element
0	-Inf
0=1	0
1	1
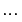q-2 where q = pm	q-2

Although -Inf is the standard exponential representation of the zero element, all negative integers are equivalent to -Inf when used as input arguments in exponential format. This equivalence can be useful; for example, see the concise line of code at the end of the section Default Primitive Polynomials.

Note    The equivalence of all negative integers and -Inf as exponential formats means that, for example, -1 does not represent -1, the multiplicative inverse of . Instead, -1 represents the zero element of the field.

Polynomial Format

The polynomial format uses the property that every element of GF(p^m) can be expressed as a polynomial in with exponents between 0 and m-1, and coefficients in GF(p). In the polynomial format, the element

A(1) + A(2) +A(3)² + ... + A(m) ^m-1

is represented in MATLAB by the vector

[A(1) A(2) A(3) ... A(m)]

Note    The Galois field functions in this toolbox represent a polynomial as a vector that lists the coefficients in order of ascending powers of the variable. This is the opposite of the order that other MATLAB functions use.

List of All Elements of a Galois Field

Some Galois field functions in this toolbox require an argument that lists all elements of an extension field GF(p^m). This is again relative to a particular primitive element of GF(p^m). The proper format for the list of elements is that of a matrix having p^m rows, one for each element of the field. The matrix has m columns, one for each coefficient of a power of in the polynomial format shown in Polynomial Format above. The first row contains only zeros because it corresponds to the zero element in GF(p^m). If k is between 2 and p^m, then the kth row specifies the polynomial format of the element ^k-2.

The minimal polynomial of aids in the computation of this matrix, since it tells how to express ^m in terms of lower powers of . For example, the table below lists the elements of GF(3²), where is a root of the primitive polynomial 2 + 2x + x². This polynomial allows repeated use of the substitution

² = -2 - 2=1+

when performing the computations in the middle column of the table.

Table 2-11: Elements of GF(9) 

Exponential Format	Polynomial Format	Row of MATLAB Matrix of Elements
-Inf	0	0 0
0	1	1 0
1		0 1
2	1+	1 1
3	+ 2 =  + 1 +  = 1 + 2	1 2
4	+ 22 =  + 2 + 2 = 2	2 0
5	2	0 2
6	22 = 2 + 2	2 2
7	2 + 22 = 2 + 2 + 2 = 2 +	2 1

An automatic way to generate the matrix whose rows are in the third column of the table above is to use the code below.

p = 3; m = 2;
% Use the primitive polynomial 2 + 2x + x^2 for GF(9).
primpoly = [2 2 1];
field = gftuple([-1:p^m-2]',primpoly,p);

The gftuple function is discussed in more detail in Converting and Simplifying Element Formats.

Nonuniqueness of Representations

A given field has more than one primitive element. If two primitive elements have different minimal polynomials, then the corresponding matrices of elements will have their rows in a different order. If the two primitive elements share the same minimal polynomial, then the matrix of elements of the field is the same.

Note    You may use whatever primitive element you want, as long as you understand how the inputs and outputs of Galois field functions depend on the choice of some primitive polynomial. It is usually best to use the same primitive polynomial throughout a given script or function.

Other ways in which representations of elements are not unique arise from the equations that Galois field elements satisfy. For example, an exponential format of 8 in GF(9) is really the same as an exponential format of 0, since ⁸=1=⁰ in GF(9). As another example, the substitution mentioned just before Table 2-11, Elements of GF(9), shows that the polynomial format [0 0 1] is really the same as the polynomial format [1 1].

Galois Field Terminology

Default Primitive Polynomials