Communications Toolbox

rsencode

Reed-Solomon encoding using the exponential format

Syntax

code = rsencode(msg,genpoly,n);
code = rsencode(msg,genpoly,n,m);
code = rsencode(msg,genpoly,n,field);

Description

For All Syntaxes

The decoding counterpart for this function is rsdecode.

rsencode uses the exponential format to represent elements of GF(2^m). For example, an entry of 2 represents the element 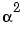, where 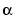is a primitive element of GF(2^m). If field is not used as an input argument, then the exponential format is relative to a root of MATLAB's default primitive polynomial for GF(2^m).If field is used as an input argument, then its format and the formats in msg and code are all relative to the same primitive element of GF(2^m). See Representing Elements of Galois Fields for more information about these formats.

Since GF(2^m) has 2^m elements, each codeword represents 2^m(2^m-1) bits of information. Each decoded message represents 2^m*k bits of information.

For Specific Syntaxes

code = rsencode(msg,genpoly,n) encodes the message msg using the Reed-Solomon coding method. n, the codeword length, must have the form 2^m-1 for some integer m greater than or equal to 3. If the message length is k, then msg is a matrix having k columns. Each entry of msg represents an element of GF(2^m) in exponential format. Each row of msg is treated as a separate message. Each row of code represents a codeword, and each entry is the exponential format of an element of GF(2^m). The last k columns of code are just msg; that is, the parity bits are at the beginning of each codeword. genpoly is a row vector that gives the coefficients, in order of ascending powers, of the generator polynomial. Each coefficient is specified in exponential format.

code = rsencode(msg,genpoly,n,m) is the same as code = rsencode(msg,genpoly,2^m-1) when m is an integer greater than or equal to 3. Specifying m as a fourth input argument speeds the execution.

code = rsencode(msg,genpoly,n,field) is the same as the first syntax, except that field is a matrix that lists the elements of GF(2^m) in the format described in List of All Elements of a Galois Field. This syntax is faster than the first one.

Examples

The commands below use the third syntax of rsencode to encode two messages.

m = 3; n = 2^m-1; % Codeword length is 7.
field = gftuple([-1:2^m-2]',m,2); % List of elements in GF(2^m)
msg = [5 0 1; 2 3 4];
k = size(msg,2); % Message length = number of columns of msg
genpoly = rspoly(n,k,field); % Generator polynomial
code = rsencode(msg,genpoly,n,field);

The reference page for rsdecode continues this example by corrupting the code and then decoding it.

See Also
rsdecode, encode, decode, rspoly, rsdeco

rsenco

rsencof