Communications Toolbox

rspoly

Produce Reed-Solomon code generator polynomial

Syntax

genpoly = rspoly(n,k);
genpoly = rspoly(n,k,m);
genpoly = rspoly(n,k,field);
[genpoly,t] = rspoly(...);

Description

genpoly = rspoly(n,k) finds the generator polynomial of a Reed-Solomon code with codeword length n and message length k. genpoly is a row vector that represents the coefficients of the generator polynomial in order of ascending powers. Each coefficient is an element of GF(2^m) represented in exponential format, as described in the section Representing Elements of Galois Fields.

genpoly = rspoly(n,k,m) is the same as genpoly = rspoly(2^m-1,k), but faster. If n does not equal 2^m-1, then an error results.

genpoly = rspoly(n,k,field) is the same as the first syntax listed, except that field indirectly specifies the primitive element for GF(2^m) relative to which the coefficients in genpoly are expressed. field is a matrix that lists the elements of GF(2^m) in the format described in List of All Elements of a Galois Field. Both field and genpoly use exponential formats relative to the same primitive element. This syntax is faster than the first syntax listed.

[genpoly,t] = rspoly(...) returns in t the error-correction capability of the Reed-Solomon code.

Examples

The command below shows that the (15, 11) Reed-Solomon code generator polynomial is

.

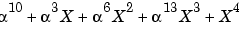genpoly = rspoly(15,11,4)

genpoly =

    10     3     6    13     0

The syntax below uses field as the third input argument in rspoly and obtains the same result.

m = 4;
field = gftuple([-1:2^m-2]',m,2);
genpoly2 = rspoly(15,11,field)

genpoly2 =

    10     3     6    13     0

See Also
encode, decode, rsenco, rsdeco

rsencof

scatterplot