

| Communications Toolbox |   |
Arithmetic in Galois Fields
You can add, subtract, multiply, and divide elements of Galois fields using the functions gfadd, gfsub, gfmul, and gfdiv, respectively. Each of these functions has a mode for prime fields and a mode for extension fields.
Arithmetic in Prime Fields
Arithmetic in GF(p) is the same as arithmetic modulo p. The functions gfadd, gfmul, gfsub, and gfdiv accept two arguments that represent elements of GF(p) as integers between 0 and p-1. An optional third argument specifies p; if it does not appear, then the computations are performed in GF(2).
Example: Addition Table for GF(5). The code below constructs an addition table for GF(5). If a and b are between 0 and 4, then the element gfp_add(a+1,b+1) represents the sum a+b in GF(5). For example, gfp_add(3,5) = 1 because 2+4 is 1 modulo 5.
p = 5;
row = 0:p-1;
table = ones(p,1)*row;
gfp_add = gfadd(table,table',p)
gfp_add =
0 1 2 3 4
1 2 3 4 0
2 3 4 0 1
3 4 0 1 2
4 0 1 2 3
Other values of p produce tables for different prime fields GF(p). Replacing gfadd by gfmul, gfsub, or gfdiv produces a table for the corresponding arithmetic operation in GF(p).
Arithmetic in Extension Fields
The same arithmetic functions can add elements of GF(pm) when m > 1, but the format of the arguments is more complicated than in the case above. In general, arithmetic in extension fields is more complicated than arithmetic in prime fields; see the works listed in Selected Bibliography for Galois Fields for details about how the arithmetic operations work.
When working in extension fields, the functions gfadd, gfmul, gfsub, and gfdiv use the first two arguments to represent elements of GF(pm) in exponential format. The third argument, which is required, lists all elements of GF(pm) as described in the section, List of All Elements of a Galois Field. The result is in exponential format.
Example: Addition Table for GF(9). The code below constructs an addition table for GF(32), using exponential formats relative to a root of the default primitive polynomial for GF(9). If a and b are between -1 and 7, then the element gfpm_add(a+2,b+2) represents the sum of 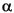 a and
a and 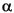 b in GF(9). For example,
b in GF(9). For example, gfpm_add(4,6) = 5 because
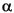 2 +
2 + 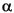 4 =
4 = 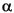 5
5
Using the fourth and sixth rows of the matrix field, you can verify that
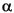 2 +
2 + 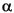 4 = (1 + 2
4 = (1 + 2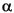 )+ (2 + 0
)+ (2 + 0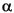 ) = 3 + 2
) = 3 + 2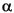 =0 + 2
=0 + 2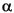 =
=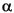 5 modulo 3.
5 modulo 3.
p = 3; m = 2; % Work in GF(3^2).
field = gftuple([-1:p^m-2]',m,p); % Construct list of elements.
row = -1:p^m-2;
table = ones(p^m,1)*row;
gfpm_add = gfadd(table,table',field)
gfpm_add =
-Inf 0 1 2 3 4 5 6 7
0 4 7 3 5 -Inf 2 1 6
1 7 5 0 4 6 -Inf 3 2
2 3 0 6 1 5 7 -Inf 4
3 5 4 1 7 2 6 0 -Inf
4 -Inf 6 5 2 0 3 7 1
5 2 -Inf 7 6 3 1 4 0
6 1 3 -Inf 0 7 4 2 5
7 6 2 4 -Inf 1 0 5 3
Other values of p and m produce tables for different prime fields GF(pm). Replacing gfadd by gfmul, gfsub, or gfdiv produces a table for the corresponding arithmetic operation in GF(pm).
 | Converting and Simplifying Element Formats | Polynomials over Prime Fields |  |