Polynomials over Prime Fields (Communications Toolbox)

Communications Toolbox

Polynomials over Prime Fields

A polynomial over GF(p) is a polynomial whose coefficients are elements of GF(p). The Communications Toolbox provides functions for:

Changing polynomials in cosmetic ways

Performing polynomial arithmetic

Characterizing polynomials as primitive or irreducible

Finding roots of polynomials in a Galois field

Note The Galois field functions in this toolbox represent a polynomial as a vector that lists the coefficients in order of ascending powers of the variable. This is the opposite of the order that other MATLAB functions use.

Cosmetic Changes of Polynomials

To display the traditionally formatted polynomial that corresponds to a row vector containing coefficients, use gfpretty. To truncate a polynomial by removing all zero-coefficient terms that have exponents higher than the degree of the polynomial, use gftrunc. For example,

polynom = gftrunc([1 20 394 10 0 0 29 3 0 0])

polynom =

     1    20   394    10     0     0    29     3

gfpretty(polynom)

                                   2       3       6      7
                   1 + 20 X + 394 X  + 10 X  + 29 X  + 3 X

Note If you do not use a fixed-width font, then the spacing in the display might not look correct.

Polynomial Arithmetic

The functions gfadd and gfsub add and subtract, respectively, polynomials over GF(p). The gfconv function multiplies polynomials over GF(p). The gfdeconv function divides polynomials in GF(p), producing a quotient polynomial and a remainder polynomial. For example, the commands below show that 2 + x + x² times 1 + x over the field GF(3) is 2 + 2x² + x³.

a = gfconv([2 1 1],[1 1],3)

a =

     2     0     2     1

[quot, remd] = gfdeconv(a,[2 1 1],3)

quot =

     1     1

remd =

     0

The previously discussed functions gfadd and gfsub add and subtract, respectively, polynomials. Because it uses a vector of coefficients to represent a polynomial, MATLAB does not distinguish between adding two polynomials and adding two row vectors elementwise.

Characterization of Polynomials

Given a polynomial over GF(p), the gfprimck function determines whether it is irreducible and/or primitive. By definition, if it is primitive then it is irreducible; however, the reverse is not necessarily true.

Given an element of GF(p^m), the gfminpol function computes its minimal polynomial over GF(p).

For example, the code below reflects the irreducibility of all minimal polynomials. However, the minimal polynomial of a nonprimitive element is not a primitive polynomial.

p = 2; m = 4;
% Use default primitive polynomial here.

primpoly = gfminpol(1,m,p);
ckprim = gfprimck(primpoly,p);
% ckprim = 1, since primpoly represents a primitive polynomial.

notprimpoly = gfminpol(3,m,p);
cknotprim = gfprimck(notprimpoly,p);
% cknotprim = 0 (irreducible but not primitive)
% since alpha^3 is not a primitive element when p = 2.

ckreducible = gfprimck([0 1 1],p);
% ckreducible = -1 since the polynomial is reducible.

Roots of Polynomials

Given a polynomial over GF(p), the gfroots function finds the roots of the polynomial in a suitable extension field GF(p^m). If p is not specified, then the default is 2. If m is not specified, then the default is the degree of the polynomial. There are two ways to tell MATLAB the degree m of the extension field GF(p^m), as shown in the table below.

Table 2-13: Formats for Second Argument of gfroots
Second Argument
Represents

A positive integer
m as in GF(p^m). MATLAB uses the default primitive polynomial in its computations.

A row vector
a primitive polynomial for GF(p^m). Here m is the degree of this primitive polynomial.

**Table 2-13: Formats for Second Argument of gfroots**
Second Argument	Represents
A positive integer	m as in GF(p^m). MATLAB uses the default primitive polynomial in its computations.
A row vector	a primitive polynomial for GF(p^m). Here m is the degree of this primitive polynomial.

Example: Roots of a Polynomial in GF(9). The code below finds roots of the polynomial 1 + x² + x³ in GF(9) and then checks that they are indeed roots. The exponential format of elements of GF(9) is used throughout.

p = 3; m = 2;
field = gftuple([-1:p^m-2]',m,p); % List of all elements of GF(9)
% Use default primitive polynomial here.
polynomial = [1 0 1 1]; % 1 + x^2 + x^3
roots =gfroots(polynomial,m,p) % Find roots in exponential format
% Check that each one is actually a root.
for ii = 1:3
   root = roots(ii);
   rootsquared = gfmul(root,root,field);
   rootcubed = gfmul(root,rootsquared,field);
   answer(ii)=...
      gfadd(gfadd(0,rootsquared,field),rootcubed,field);
   % Recall that 1 is really alpha to the zero power.
   % If answer = -Inf, then the variable root represents
   % a root of the polynomial.
end
answer

The output shows that 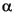⁰ (which equals 1), 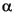⁵, and 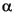⁷ are roots.

roots =

     0
     5
     7


answer =

  -Inf  -Inf  -Inf

See the reference page for gfroots to see how gfroots can also provide you with the polynomial formats of the roots and the list of all elements of the field.

Arithmetic in Galois Fields Other Galois Field Functions