Communications Toolbox

Converting and Simplifying Element Formats

This section describes how to convert between the exponential and polynomial formats for Galois field elements, as well as how to simplify a given representation.

Converting to Simplest Polynomial Format

The gftuple function produces the simplest polynomial representation of an element of GF(p^m), given either an exponential representation or a polynomial representation of that element. This can be useful for generating the list of elements of GF(p^m) that other functions require.

The simplest use of gftuple requires two arguments: one representing an element of GF(p^m) and the other indicating the primitive polynomial that MATLAB should use when computing the output. An optional third argument is the prime p; if it is omitted, then the default is 2. The table below indicates how gftuple behaves when given the first two arguments in various formats.

Table 2-12: Behavior of gftuple Depending on Format of Inputs 

How to Specify Element	How to Indicate Primitive Polynomial	What gftuple Produces
Exponential format; c = any integer	Integer m > 1	Polynomial format of c, where is a root of the default primitive polynomial for GF(pm)
Example: tp = gftuple(6,2,3); % c = 6 here
Exponential format; c = any integer	Vector of coefficients of primitive polynomial	Polynomial format of c, where is a root of the given primitive polynomial
Example: polynomial = gfprimdf(2,3); tp = gftuple(6,polynomial,3); % c = 6 here
Polynomial format of any degree	Integer m > 1	Polynomial format of degree < m, using default primitive polynomial for GF(pm) to simplify
Example: tp = gftuple([0 0 0 0 0 0 1],2,3);
Polynomial format of any degree	Vector of coefficients of primitive polynomial	Polynomial format of degree < m, using the given primitive polynomial for GF(pm) to simplify
Example: polynomial = gfprimdf(2,3); tp = gftuple([0 0 0 0 0 0 1],polynomial,3);

The four examples that appear in the table above all produce the same vector tp = [2, 1], but their different inputs to gftuple correspond to the lines of the table. Each example expresses the fact that

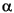⁶ = 2+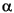

where 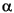is a root of the (default) primitive polynomial 2 + x + x² for GF(3²).

Example.   This example shows how gfconv and gftuple combine to multiply two polynomial-format elements of GF(3⁴). Initially, gfconv multiplies the two polynomials, treating the primitive element as if it were a variable. This produces a high-order polynomial, which gftuple simplifies using the polynomial equation that the primitive element satisfies. The final result is the simplest polynomial format of the product.

p = 3; m = 4;
a = [1 2 0 1]; b = [2 2 1 2];
notsimple = gfconv(a,b,p) % a times b, using high powers of alpha

notsimple =

     2     0     2     0     0     1     2
simple = gftuple(notsimple,m,p) %Highest exponent of alpha is m-1

simple =

     2     1     0     1

Example: Generating a List of Galois Field Elements

This example applies the conversion functionality to the task of generating a matrix that lists all elements of a Galois field. A matrix that lists all field elements is an input argument in functions such as gfadd and gfmul. The variables field1 and field2 below have the format that such functions expect.

p = 5; % Or any prime number
m = 4; % Or any positive integer
field1 = gftuple([-1:p^m-2]',m,p);
primpoly = gfprimdf(m,p); % Or any primitive polynomial
% for GF(p^m)
field2 = gftuple([-1:p^m-2]',primpoly,p);

Converting to Simplest Exponential Format

The same function gftuple also produces the simplest exponential representation of an element of GF(p^m), given either an exponential representation or a polynomial representation of that element. To retrieve this output, use the syntax

[polyformat, expformat] = gftuple(...)

The input format and the output polyformat are as in Table 2-12, Behavior of gftuple Depending on Format of Inputs. In addition, the variable expformat contains the simplest exponential format of the element represented in polyformat. It is simplest in the sense that the exponent is either -Inf or a number between 0 and p^m-2.

To recover the exponential format of the element 2 + 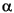 that the previous section considered, use the commands below. In this case, polyformat contains redundant information, while expformat contains the desired result.

[polyformat, expformat] = gftuple([2 1],2,3)

polyformat =

     2     1

expformat =

     6

This output appears at first to contradict the information in Table 2-11, Elements of GF(9), but in fact it does not. The table uses a different primitive element; two plus that primitive element has the polynomial and exponential formats shown below. The output below reflects the information in the bottom line of the table.

primpoly = [2 2 1];
[polyformat, expformat] = gftuple([2 1],primpoly,3)

polyformat =

     2     1


expformat =

     7

Default Primitive Polynomials

Arithmetic in Galois Fields