| Spline Toolbox | |
Syntax
sp = spaps(x,y,tol)[sp, values, rho] = spaps(x,y,tol,arg1,arg2)
Description
Returns the smoothest function that lies within the given tolerance tol of the given data and, optionally, its values at the given x.
Here, smoothest means that the following roughness measure is minimized:
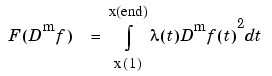
Further, the distance of the function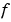 
from the given data is measured by
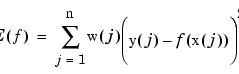
The default value for m is 2, leading to the cubic smoothing spline. However, the choices m=1, for the linear smoothing spline, and m=3, for the quintic, smoothing spline, are available, too, by setting one of the optional inputs argi equal to 1 or 3. Further, the default value for the weight vector w makes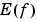 
the composite trapezoidal rule approximation to
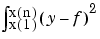. But the weight vector may also be supplied as one of the optional inputs argi (as a positive vector of the same length as x). Finally, the default for the piecewise constant nonnegative weight function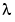 
in the roughness measure is 1, but its constant value on the interval (x(i-1) .. x(i)) may also be supplied as the i-th entry, i=2:length(x), of the vector tol, in which case tol(1) continues to be used as the specified tolerance.
The spline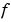 
is determined as the unique minimizer of the expression 
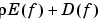, with the smoothing parameter 
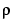(optionally returned) so chosen that 
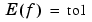in case tol is nonnegative; in the contrary case,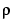 
is taken to be -tol. Hence, when m is 2, then, after conversion to ppform, the result should be the same (up to roundoff) as obtained by csaps(x,y,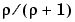 
).
If x is not increasing, then both x and y (as well as w if given) will be reordered in concert to make x increasing. After that, x must be strictly increasing.
The data being fitted may be d-vector-valued, and this is indicated by having y be of size [d,n]. In this case, both the measure of roughness and the distance of the (d-vector-valued) function f from the data are the sum of the componentwise measures. For example, if f(x) is the d-vector (f1(x), ...,fd(x)), then E(f) = E(f1) + ... + E(fd).
It is also possible to obtain a smoothing spline for gridded data. When x is a cell array of length r, then y is expected to supply the corresponding gridded values, with size(y) equal to [length(x{1}),...,length(x{r})] in case the function is scalar-valued, and equal to [d,length(x{1}),...,length(x{r})] in case the function is d-vector-valued. Further, the optional input for m must be an r-vector (with entries from the set {1,2,3}), and the optional argument for w must be a cell array of length r, with w{i} either empty (to indicate that the default choice is wanted) or else a positive vector of the same length as x{i}.
Examples
w = ones(size(x)); w([1 end]) = 100;
sp = spaps(x,y, 1.e-2, w, 3);
give a quintic smoothing spline approximation to the given data that close to interpolates the first and last datum, while being within about 1.e-2 of the rest.
Algorithm
Reinsch's approach [1] is used (including his clever way of choosing the equation for the optimal smoothing parameter in such a way that a good initial guess is available and Newton's method is guaranteed to converge and to converge fast).
See Also
References
[1] C. Reinsch, ``Smoothing by spline functions'', Numer. Math. 10 (1967), 177-183.
| | spapi | spcol | |