| Spline Toolbox | |
Syntax
spline = spapi(knots,x,y) spline = spapi(k,x,y)
Description
Returns the spline f (if any) of order
k = length(knots) - length(x)
with knot sequence knots for which
(*)y(:,i)= f(x(i)), alli.
This is taken in the osculatory sense in case some x are repeated, i.e., in the sense that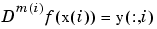 
in case the x are in nondecreasing order, with m = knt2mlt(x), i.e., m(i) := #{j < i:x(j) = x(i)}. Thus m-fold repetition of a site z in x corresponds to the prescribing of value and the first m - 1 derivatives of f at z.
It is possible to merely specify the desired spline order, k, as the first argument instead of the knot sequence, knots, in which case aptknt is used to determine a workable (though not necessarily optimal) knot sequence for the given sites x.
It is also possible to interpolate to gridded data. If knots is a cell array with m entries, then also x must be a cell array with m entries, and y must be an (m+1)-dimensional array, with y(:,i1,...,im) the datum to be fitted at the m-vector [x{1}(i1),...,x{m}(im)], all i1, ..., im , unless the spline is to be scalar-valued, in which case, in contrast to the univariate case, y is permitted to be an m-dimensional array.
Examples
spapi([0 0 0 0 1 2 2 2 2],[0 1 1 1 2],[2 0 1 2 -1])produces the unique cubic spline f on [0..2] with exactly one interior knot, at 1, that satisfies the five conditions
f(0+) = 2, f(1) = 0, Df(1) = 1, D2f(1) = 2, f(2-) = -1
Since the given values are reordered in concert with the given sites if the latter are not already in nondecreasing order, it is, e.g., possible to carry out interpolation to values y and slopes s at the increasing site sequence x by a quintic spline by the command
sp = spapi(augknt(x,6,2),[x x x([1 end])],[y,s,ddy0,ddy1]);
with ddy0 and ddy1 values for the second derivative at the endpoints.
As a related example, if the function sin(x) is to interpolated at the distinct data sites x by a cubic spline and its slope is also to be matched at a subsequence x(s), then this can be accomplished by the command
sp = spapi(4,[x x(s)], [sin(x) cos(x(s))]);
in which a suitable knot sequence is supplied iwth ahe aid of aptknt. In fact, if you wanted to interpolate the same data by quintic splines, simply change the 4 to 6. The command spapi(k,x,y) has the same effect as the more explicit command spapi(aptknt(x,k),x,y).
As a final example, here is the bivariate interpolant.
x = -2:.5.2; x=-1:.25:1; [xx, yy] = ndgrid(x,y);
z = exp(-(xx.^2+yy.^2));
sp = spapi({3,4},{x,y},z); fnplt(sp)
The command spapi(k,x,y) has the same effect as the more explicit command spapi(aptknt(x,k),x,y).
Algorithm
spcol is called on to provide the almost-block-diagonal collocation matrix (Bj,k(x)) (with repeats in x denoting derivatives, as described above), and slvblk solves the linear system (*), using a block QR factorization.
Gridded data are fitted, in tensor-product fashion, one variable at a time, taking advantage of the fact that a univariate spline fit depends linearly on the values being fitted.
See Also
Limitations
The given (univariate) knots and sites must satisfy the Schoenberg-Whitney conditions for the interpolant to be defined. Assuming the site sequence x to be nondecreasing, this means that we must have
knots(j) <x(j) < knots(j+k), all j,
(with equality possible at knots(1) and knots(end)). In the multivariate case, these conditions must hold in each variable separately.
Cautionary Note
If the (univariate) sequence x is not nondecreasing, both x and y will be reordered in concert to make it so. In the multivariate case, this is done in each variable separately. A positive side effect of this was noted above in the examples.
| | spap2 | spaps | |