

| Spline Toolbox |   |
Least-squares spline approximation
Syntax
sp = spap2(knots,k,x,y) sp = spap2(l,k,x,y) sp = spap2(knots,k,x,y,w)
Description
Returns the spline f of order k with knot sequence knots for which
(*)y(:,j) = f(x(j)), allj
in the weighted mean-square sense, meaning that the sum
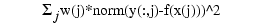 is minimized, with default weights equal to 1. If the sites
is minimized, with default weights equal to 1. If the sites x satisfy the (Schoenberg-Whitney) conditions
(**)knots(j)< x(j)< knots(j +k) j=1,...,length(x)=length(knots)-k
then there is a unique spline (of the given order and knot sequence) satisfying (*) exactly. No spline is returned unless (**) is satisfied for some subsequence of x.
Since the proper choice of the knot sequesnce may be a challenge at times, it is also acceptable to input, instead of the sequence knots, the integer 1 giving the number of polynomial pieces to be used, in which case spap2 provides a knot sequence suitable for that.
It is also possible to fit to gridded data. If knots is a cell array with m entries, then also x must be a cell array with m entries, as must w be (if given). Further, then also k must be an m-vector, and y must be an (m+1)-dimensional array, with y(:,i1,...,im) the datum to be fitted at the m-vector [x{1}(i1),...,x{m}(im)], all i1, ..., im. However, if the spline is to be scalar-valued, then, in contrast to the univariate case, y is permitted to be an m-dimensional array, in which case y(i1,...,im) the datum to be fitted at the m-vector [x{1}(i1),...,x{m}(im)], all i1, ..., im.
Examples
sp = spap2(augknt([a,xi,b],4),4,x,y)
is the least-squares approximant to the data x, y, by cubic splines with two continuous derivatives, basic interval [a..b], and interior breaks xi, provided xi has all its entries in (a..b) and the conditions (**) are satisfied in some fashion. In that case, the approximant consists of l=length(xi)+1 polynomial pieces. If you do not want to worry about the conditions (**) but merely want to get a cubic spline approximant consisting of 1 polynomial pieces, use instead
sp = spap2(1,4,x,y);
If the resulting approximation is not satisfactory, try using a larger 1. Else use
sp = spap2(newknt(sp),4,x,y);
for a possible better distribution of the knot sequence. In fact, if that helps, repeating it may help even more.
As another example, spap2(1, 2, x, y); provides the least-squares straight-line fit to data x,y, while
w = ones(size(x)); w([1 end]) = 100; spap2(1,2, x,y,w);
forces that fit to come very close to the first data point and to the last.
Algorithm
spcol is called on to provide the almost block-diagonal collocation matrix 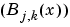 , and
, and slvblk solves the linear system (*) in the (weighted) least-squares sense, using a block QR factorization.
If only the number of polynomial pieces is specified, then an appropriate knot sequence is obtained by applying aptknt to an appropriate subsequence of the data sites x.
Gridded data is fitted, in tensor-product fashion, one variable at a time, taking advantage of the fact that a univariate weighted least-squares fit depends linearly on the values being fitted.
See Also
 | sorted | spapi |  |