| Spline Toolbox | |
Syntax
[values,p] = csaps(x,y,p,xx) [values,p] = csaps(x,y,p,xx,w) [pp,p] = csaps(x,y) [pp,p] = csaps(x,y,p) [pp,p] = csaps(x,y,p,[],w)
Description
The cubic smoothing spline s to the given data x,y is constructed, for the specified smoothing parameter p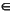 
[0..1] and the optionally specified weight w. If the smoothing parameter is negative or none is specified, p is chosen in the "interesting range" discussed below; in any case, the value of p used is returned as the optional second output argument.
The smoothing spline minimizes
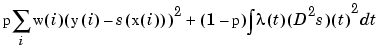
with w=ones(size(x)) the default value for the weight vector w in the error measure, and 1 the default for the piecewise constant weight function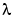 
in the roughness measure. For p = 0, s is the least-squares straight line fit to the data, while, on the other extreme, i.e., for p = 1, s is the variational, or `natural' cubic spline interpolant. As p moves from 0 to 1, the smoothing spline changes from one extreme to the other. The interesting range of p is often near 1/(1+h3/6), with h the average spacing of the data sites. For uniformly spaced data, one would expect a close following of the data for p = 1/(1 + h3/60) and some satisfactory smoothing for p = 1/(1 + h3/.6).
The call csaps(x,y,p,xx) and csaps(x,y,p,xx,w) return the values s(xx) of this cubic smoothing spline at the given argument sequence xx instead of the smoothing spline itself.
The alternative call csaps(x,y,p) returns instead the ppform of the cubic spline, for later use with fnval, fnder, etc.
It is in general difficult to choose the parameter p without experimentation (such as specifying a negative p on a first try). For that reason, use of spaps is encouraged since there p is (implicitly) chosen so as to produce the smoothest spline within a specified tolerance of the data.
The weight function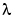 
in the roughness measure can, optionally, be specified as a (non-negative) piecewise constant function, with breaks at the data sites x , by inputing for p a vector whose i-th entry provides the value of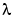 
on the interval (x(i-1) .. x(i)) for i=2:length(x). The first entry of the input vector p continues to be used as the desired value of the smoothness parameter p. In this way, it is possible to insist that the resulting smoothing spline be smoother in some parts of the interval than in others.
It is also possible to smooth data on a rectangular grid and obtain smoothed values on a rectangular grid or at scattered sites, by the calls
values = csaps( {x1,...,xm}, y, p, xx, w)
pp = csaps( {x1,...,xm}, y, p, [], w )
in which y is expected to have size [d,length(x1),...,.length(xm)] (or [length(x1),...,.length(xm)] if the function is to be scalar-valued), and p is either a scalar or an m-vector of scalars, and xx is either a list of m-vectors xx(:,j) or else a cell-array {xx1,..., xxm} specifying the m-dimensional grid at which to evaluate the interpolant, and, correspondingly, w, if given, is cell array of weight sequences for the m dimensions (with w{i} empty the indication that the default weights are to be used with the ith variable).
Algorithm
This is an implementation of the Fortran routine SMOOTH from PGS.
See Also
Cautionary Note
If the sequence x is not nondecreasing, both x and y will be reordered in concert to make it so.
| | csapi | cscvn | |