| Optimization Toolbox | |
Levenberg-Marquardt Implementation
The main difficulty in the implementation of the Levenberg-Marquardt method is an effective strategy for controlling the size of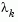 
at each iteration so that it is efficient for a broad spectrum of problems. The method used in this implementation is to estimate the relative nonlinearity of f(x) using a linear predicted sum of squares 
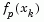and a cubicly interpolated estimate of the minimum 
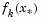. In this way the size of
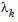is determined at each iteration.
The linear predicted sum of squares is calculated as
|
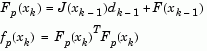
(2-23) |
and the term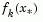 
is obtained by cubicly interpolating the points 
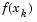and 
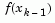. A step length parameter 
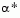is also obtained from this interpolation, which is the estimated step to the minimum. If 
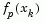is greater than 
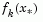, then 
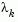is reduced, otherwise it is increased. The justification for this is that the difference between 
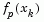and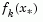 
is a measure of the effectiveness of the Gauss-Newton method and the linearity of the problem. This determines whether to use a direction approaching the steepest descent direction or the Gauss-Newton direction. The formulas for the reduction and increase in 
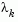, which have been developed through consideration of a large number of test problems, are shown in Figure 2-5, Updating 
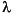k below.
Following the update of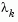 
, a solution of Eq. 2-22 is used to obtain a search direction, 
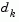. A step length of unity is then taken in the direction 
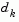, which is followed by a line search procedure similar to that discussed for the unconstrained implementation. The line search procedure ensures that 
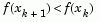at each major iteration and the method is therefore a descent method.
The implementation has been successfully tested on a large number of nonlinear problems. It has proved to be more robust than the Gauss-Newton method and iteratively more efficient than an unconstrained method. The Levenberg-Marquardt algorithm is the default method used by lsqnonlin. The Gauss-Newton method can be selected by setting the options parameter LevenbergMarquardt to 'off'.
| | Gauss-Newton Implementation | Constrained Optimization | |
