Optimization Toolbox

Levenberg-Marquardt Method

The Levenberg-Marquardt [25],[27] method uses a search direction that is a solution of the linear set of equations

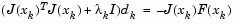
(2-22)

where the scalar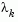 controls both the magnitude and direction of 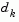. When 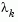is zero, the direction 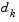is identical to that of the Gauss-Newton method. As 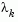tends to infinity, 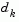tends towards a vector of zeros and a steepest descent direction. This implies that for some sufficiently large 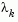, the term 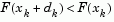holds true. The term 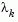can therefore be controlled to ensure descent even when second order terms, which restrict the efficiency of the Gauss-Newton method, are encountered.

The Levenberg-Marquardt method therefore uses a search direction that is a cross between the Gauss-Newton direction and the steepest descent. This is illustrated in Figure 2-4, Levenberg-Marquardt Method on Rosenbrock's Function below. The solution for Rosenbrock's function (Eq. 2-2) converges after 90 function evaluations compared to 48 for the Gauss-Newton method. The poorer efficiency is partly because the Gauss-Newton method is generally more effective when the residual is zero at the solution. However, such information is not always available beforehand, and occasional poorer efficiency of the Levenberg-Marquardt method is compensated for by its increased robustness.

Figure 2-4: Levenberg-Marquardt Method on Rosenbrock's Function

Gauss-Newton Method

Nonlinear Least Squares Implementation