| Optimization Toolbox | |
Gauss-Newton Implementation
The Gauss-Newton method is implemented using similar polynomial line search strategies discussed for unconstrained optimization. In solving the linear least squares problem (Prob. 2.18), exacerbation of the conditioning of the equations is avoided by using the QR decomposition of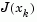 
and applying the decomposition to 
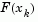(using the MATLAB \ operator). This is in contrast to inverting the explicit matrix, 
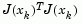, which can cause unnecessary errors to occur.
Robustness measures are included in the method. These measures consist of changing the algorithm to the Levenberg-Marquardt method when either the step length goes below a threshold value (in this implementation 1e-15) or when the condition number of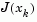 
is below 1e-10. The condition number is a ratio of the largest singular value to the smallest.
| | Nonlinear Least Squares Implementation | Levenberg-Marquardt Implementation | |