Communications Toolbox

gfminpol

Find the minimal polynomial of an element of a Galois field

Syntax

pol = gfminpol(k,m);
pol = gfminpol(k,primpoly);
pol = gfminpol(k,m,p);
pol = gfminpol(k,primpoly,p);

Description

pol = gfminpol(k,m) finds the minimal polynomial of 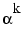over GF(2), where 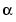is a root of the default primitive polynomial for GF(2^m). m is an integer greater than one. The format of the output is listed below:

• If k is a nonnegative integer, then pol is a row vector that gives the coefficients of the minimal polynomial in order of ascending powers.
• If k is a vector of length len all of whose entries are nonnegative integers, then pol is a matrix having len rows; the rth row of pol gives the coefficients of the minimal polynomial of 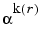in order of ascending powers.

pol = gfminpol(k,primpoly) is the same as the first syntax listed, except that 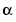is a root of the primitive polynomial for GF(2^m) specified by primpoly. primpoly is a row vector that gives the coefficients of the degree-m primitive polynomial in order of ascending powers.

pol = gfminpol(k,m,p) is the same as the first syntax listed, except that 2 is replaced by a prime number p.

pol = gfminpol(k,primpoly,p) is the same as the first syntax listed, except that 2 is replaced by a prime number p, and that 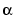is a root of the primitive polynomial for GF(p^m) specified by primpoly. primpoly is a row vector that gives the coefficients of the degree-m primitive polynomial in order of ascending powers.

Examples

The syntax gfminpol(k,m,p) is used in the sample code in the section Characterization of Polynomials.

As another example, the code below determines which elements of GF(2⁴) are also in GF(2²), by considering the degrees of their minimal polynomials.

p = 2; m = 4; % Consider elements of GF(16).
primpoly = gfprimdf(4);
% Get minimal polys for all elements except 0 and 1.
k = [1:p^m-2];
minpolys = gfminpol(k,primpoly); 

% Check which minimal polys have degree 2.
gf4=[];
for ii = 1:p^m-2
   if length(gftrunc(minpolys(ii,:)))==3 % A degree-2 polynomial
      gf4=[gf4, ii];
   end
end

disp(['The elements of GF(4) are 0, 1, alpha^',...
   int2str(gf4(1)),' and alpha^',int2str(gf4(2))])
disp('where alpha is a root in GF(16) of the polynomial')
gfpretty(primpoly)

The output is below.

The elements of GF(4) are 0, 1, alpha^5 and alpha^10
where alpha is a root in GF(16) of the polynomial
 
                                           4
                                  1 + X + X 

See Also
gfprimdf, gfcosets, gfroots

gflineq

gfmul