Spline Toolbox

Example: Construction of the Chebyshev Spline

The Chebyshev spline C = C_t = C_k,t of order k for the knot sequence t = (t_i : i=1:n+k) is the unique element of S_k,t of max-norm 1 that maximally oscillates on the interval [t_k . . t_n+1] and is positive near t_n+1. This means that there is a unique strictly increasing n-sequence 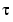so that the function 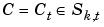given by

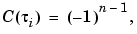all i, has max-norm 1 on [t_k . . t_n+1]. This implies that 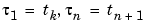, and that 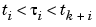, all i. In fact, 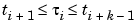, all i. This brings up the point that the knot sequence is assumed to make such an inequality possible, i.e., the elements of S_k,t are assumed to be continuous.

In short, the Chebyshev spline C looks just like the Chebyshev polynomial. It performs similar functions. For example, its extreme sites 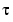are particularly good sites to interpolate at from S_k,t since the norm of the resulting projector is about as small as can be; see the toolbox command chbpnt.

In this example, which can be run via chebdem, we try to construct C for a particular knot sequence t.

We deal with cubic splines, i.e., with order

k = 4;

and use the break sequence

breaks = [0 1 1.1 3 5 5.5 7 7.1 7.2 8];
lp1 = length(breaks); 

and use simple interior knots, i.e., use the knot sequence

t = breaks([ones(1,k) 2:(lp1-1) lp1(:,ones(1,k))]);

Note the quadruple knot at each end. Since k = 4, this makes
[0..8] = [breaks(1)..breaks(lp1)] the interval [t_k..t_n+1] of interest, with
n = length(t)-k the dimension of the resulting spline space S_k,t. The same knot sequence would have been supplied by

t=augknt(breaks,k);

As our initial guess for the 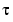, we use the knot averages

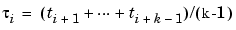
recommended as good interpolation site choices. These are supplied by

tau=aveknt(t,k); 

We plot the resulting first approximation to C, i.e., the spline c that satisfies

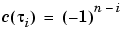, all i:

b = (-ones(1,n)).^[n-1:-1:0]; 
c = spapi(t,tau,b); 
fnplt(c,'-.') 
grid

Here is the resulting picture:

Figure 1-16: First Approximation to a Chebyshev Spline

Starting from this approximation, we use the Remez algorithm to produce a sequence of splines converging to C. This means that we construct new 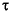as the extrema of our current approximation c to C and try again. Here is the entire loop.

We find the new interior 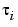as the zeros of Dc := the first derivative of c, in several steps. First, we differentiate:

cp = fnder(c);

Next, we take the zeros of the control polygon of Dc as our first guess for the zeros of Dc. For this, we must take apart the spline cp.

[knots,coefs,np,kp] = spbrk(cp);

The control polygon has the vertices (tstar(i),coefs(i)), with tstar the knot averages for the spline, provided by aveknt:

tstar = aveknt(knots,kp);

Here are the zeros of the resulting control polygon of cp:

npp = [1:np-1]; 
guess = tstar(npp) -coefs(npp).*(diff(tstar)./diff(coefs));

This provides already a very good first guess for the actual zeros.

We refine this estimate for the zeros of Dc by two steps of the secant method, taking tau and this guess as our first approximations. First, we evaluate Dc at both sets:

sites = tau(ones(4,1),2:n-1); 
sites(1,:) = guess; 
values = zeros(4,n-2); 
values(1:2,:) = reshape(fnval(cp,sites(1:2,:)),2,n-2);

Now come two steps of the secant method. We guard against division by zero by setting the function value difference to 1 in case it is zero. Since Dc is strictly monotone near the sites sought, this is harmless:

for j=2:3 
  rows = [j,j-1];cpd=diff(values(rows,:));
  cpd(find(cpd==0)) = 1; 
  sites(j+1,:) = sites(j,:) ... 
           -values(j,:).*(diff(sites(rows,:))./cpd); 
  values(j+1,:) = fnval(cp,sites(j+1,:)); 
end

The check

max(abs(values.')) 
  ans = 4.1176 5.7789 0.4644 0.1178

shows the improvement.

Now we take these sites as our new tau,

tau = [tau(1) sites(4,:) tau(n)];

and check the extrema values of our current approximation there:

extremes = abs(fnval(c, tau));

The difference

max(extremes)-min(extremes)
  ans = 0.6905

is an estimate of how far we are from total leveling.

We construct a new spline corresponding to our new choice of tau and plot it on top of the old:

c = spapi(t,tau,b); 
sites = sort([tau [0:100]*(t(n+1)-t(k))/100]); 
values = fnval(c,sites); 
hold on, plot(sites,values)

Here is the resulting picture:

Figure 1-17: A More Nearly Level Spline

If this is not close enough, one simply reiterates the loop. For this example, the next iteration already produces C to graphic accuracy.

Example: A Nonlinear ODE

Example: Approximation by Tensor Product Splines