Spline Toolbox

Example: Approximation by Tensor Product Splines

Since the toolbox can handle splines with vector coefficients, it is easy to implement interpolation or approximation to gridded data by tensor product splines, as the following illustration, run by tspdem, is meant to show.

To be sure, most tensor product spline approximation to gridded data can be obtained directly with one of the spline construction commands, like spapi or csape, in this toolbox, without concern for the details discussed in this example. Rather, this example is meant to illustrate the theory behind the tensor product construction, and this will be of help in situations not covered by the construction commands in this toolbox.

Consider, for example, least-squares approximation to given data
z(i,j) = f(x(i),y(j)), i = 1:Nx, j = 1:Ny. We take the data from a function used extensively by Franke for the testing of schemes for surface fitting (see [R. Franke, "A critical comparison of some methods for interpolation of scattered data", Naval Postgraduate School Techn. Rep. NPS-53-79-003, March 1979]). Its domain is the unit square. We choose a few more data sites in the x-direction than the y-direction; also, for a better definition, we use higher data density near the boundary.

x = sort([[0:10]/10,.03 .07, .93 .97]);
y = sort([[0:6]/6,.03 .07, .93 .97]);
[xx,yy] = ndgrid(x,y); z = franke(xx,yy);

We treat these data as coming from a vector-valued function, namely, the function of y whose value at y(j) is the vector z(:,j), all j. For no particular reason, we choose to approximate this function by a vector-valued parabolic spline, with three uniformly spaced interior knots. This means that we choose the spline order and the knot sequence for this vector-valued spline as

ky = 3; knotsy = augknt([0,.25,.5,.75,1],ky);

and then use spap2 to provide us with the least-squares approximant to the data:

sp = spap2(knotsy,ky,y,z);

In effect, we are finding simultaneously the discrete least-squares approximation from S_ky,knotsy to each of the Nx data sets

In particular, the statements

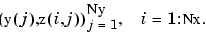
yy = [-.1:.05:1.1]; vals = fnval(sp,yy);

provide the array vals, whose entry vals(i,j) can be taken as an approximation to the value f(x(i), yy(j)) of the underlying function f at the mesh-point (x(i),yy(j)) since vals(:,j) is the value at yy(j) of the approximating spline curve in sp.

This is evident in the following figure, obtained by the command:

mesh(x,yy,vals.'), view(150,50)

Note the use of vals.', in the mesh command, needed because of MATLAB's matrix-oriented view when plotting an array. This can be a serious problem in bivariate approximation since there it is customary to think of z(i,j) as the function value at the point (x(i), y(j)), while MATLAB thinks of z(i,j) as the function value at the point (x(j), y(i)).

Figure 1-18: A Family of Smooth Curves Pretending to Be a Surface

Note that both the first two and the last two values on each smooth curve are actually zero since both the first two and the last two sites in yy are outside the basic interval for the spline in sp.

Note also the ridges. They confirm that we are plotting smooth curves in one direction only.

To get an actual surface, we now have to go a step further. Look at the coefficients coefsy of the spline in sp:

coefsy = fnbrk(sp,'c');

Abstractly, you can think of the spline in sp as the function

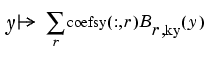
with the ith entry coefsy(l, r) of the vector coefficient coefsy(:,r) corresponding to x(i), all i. This suggests approximating each coefficient vector coefsy(r,:) by a spline of the same order kx and with the same appropriate knot sequence knotsx. Again for no particular reason, we choose this time to use cubic splines with four uniformly spaced interior knots:

kx = 4; knotsx = augknt([0:.2:1],kx); 
sp2 = spap2(knotsx,kx,x,coefsy.');

Note that spap2(knots,k,x,fx) expects fx(:,j) to be the datum at x(j), i.e., expects each column of fx to be a function value. Since we wanted to fit the datum coefsy(:,r) at x(r), all r, we had to present spap2 with the transpose of coefsy.

Now consider the transpose of the coefficients cxy of the resulting spline curve:

coefs = fnbrk(sp2,'c').';

It provides the bivariate spline approximation

to the original data

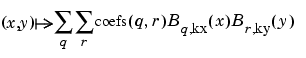
     (x(i),y(j)) z(x(i),y(j)), i=1:Nx; j=1:Ny.  

To plot this spline surface over a grid, e.g., the grid

xv = [0:.025:1]; yv = [0:.025:1];

you can do the following:

values = spcol(knotsx,kx,xv)*coefs*spcol(knotsy,ky,yv).'; 
mesh(xv,yv,values.'), view(150,50);

This results in the following figure.

Figure 1-19: Spline Approximation to Franke's Function

This makes good sense since spcol(knotsx,kx,xv) is the matrix whose (i,q)-entry equals the value B_q,kx(xv(i)) at xv(i) of the qth B-spline of order kx for the knot sequence knotsx.

Since the matrices spcol(knotsx,kx,xv) and spcol(knotsy,ky,yv) are banded, it may be more efficient, though perhaps more memory-consuming, for large xv and yv to make use of fnval, as follows:

value2 = ... 
  fnval(spmak(knotsx,fnval(spmak(knotsy,coefs),yv).'),xv).';

This is, in fact, what happens internally when fnval is called directly with a tensor product spline, as in

value2 = fnval(spmak({knotsx,knotsy},coefs),{xv,yv});

Here is the calculation of the relative error, i.e., the difference between the given data and the value of the approximation at those data sites as compared with the magnitude of the given data:

errors = z - spcol(knotsx,kx,x)*coefs*spcol(knotsy,ky,y).'; 
disp( max(max(abs(errors)))/max(max(abs(z))) ) 
0.0539

This is perhaps not too impressive. On the other hand, we used only a coefficient array of size

disp(size(coefs)) 
8 6

to fit a data array of size

disp(size(z)) 
15 11

The approach followed here seems biased, in the following way. We first think of the given data z as describing a vector-valued function of y, and then we treat the matrix formed by the vector coefficients of the approximating curve as describing a vector-valued function of x.

What happens when we take things in the opposite order, i.e., think of z as describing a vector-valued function of x, and then treat the matrix made up from the vector coefficients of the approximating curve as describing a vector-valued function of y?

Perhaps surprisingly, the final approximation is the same, up to roundoff. Here is the numerical experiment.

First, we fit a spline curve to the data, but this time with x as the independent variable, hence it is the rows of z that now become the data values. Correspondingly, we must supply z.', rather than z, to spap2,

spb = spap2(knotsx,kx,x,z.');

thus obtaining a spline approximation to all the curves (x;z(:,j)). In particular, the statement

valsb = fnval(spb,xv).';

provides the matrix valsb, whose entry valsb(i, j) can be taken as an approximation to the value f(xv(i),y(j)) of the underlying function f at the mesh-point (xv(i),y(j)). This is evident when we plot valsb using mesh:

mesh(xv,y,valsb.'), view(150,50)

Figure 1-20: Another Family of Smooth Curves Pretending to Be a Surface

Note the ridges. They confirm that we are, once again, plotting smooth curves in one direction only. But this time the curves run in the other direction.

Now comes the second step, to get the actual surface. First, extract the coefficients:

coefsx = fnbrk(spb,'c');

Then fit each coefficient vector coefsx(r,:) by a spline of the same order ky and with the same appropriate knot sequence knotsy:

spb2 = spap2(knotsy,ky,y,coefsx.');

Note that, once again, we need to transpose the coefficient array from spb, since spap2 takes the columns of its last input argument as the data values.

Correspondingly, there is now no need to transpose the coefficient array coefsb of the resulting curve:

coefsb = fnbrk(spb2,'c');

The claim is that coefsb equals the earlier coefficient array coefs, up to round-off, and here is the test:

disp( max(max(abs(coefs - coefsb))) ) 
1.4433e-15

The explanation is simple enough: The coefficients c of the spline s contained in sp = spap2(knots,k,x,y) depend linearly on the input values y. This implies, given that both c and y are 1-row matrices, that there is some matrix A = A_knots,k,x so that

c = y*A_knots,k,x

for any data y. This statement even holds when y is a matrix, of size d by N, say, in which case each datum y(:,j) is taken to be a point in d-space, and the resulting spline is correspondingly d-vector-valued, hence its coefficient array c is of size d by n, with n = length(knots)-k.

In particular, the statements

sp = spap2(knotsy,ky,y,z); 
coefsy =fnpbrk(sp,'c');

provide us with the matrix coefsy that satisfies

coefsy = z*Aknotsy,ky,y

The subsequent computations

sp2 = spap2(knotsx,kx,xx,coefsy.'); 
coefs = fnbrk(sp2,'c').';

generate the coefficient array coefs, which, taking into account the two transpositions, satisfies

coefs = ((z*Aknotsy,ky,y)' *Aknotsx,kx,x)'
      = (Aknotsx,kx,x)' *z*Aknotsy,ky,y

In the second, alternative calculation, we first computed

spb = spap2(knotsx,kx,x,z.'); 
coefsx = fnbrk(spb,'c');

hence coefsx = z'*A_knotsx,kx,x. The subsequent calculation

spb2 = spap2(knotsy,ky,y,coefsx.'); 
coefsb = fnbrk(spb,'c');

then provided

   coefsb = coefsx.' *Aknotsy,ky,y = (Aknotsx,kx,x).'*z*A_knotsy,ky,y

Consequently, coefsb = coefs.

The second approach is more symmetric than the first in that transposition takes place in each call to spap2 and nowhere else. This approach can be used for approximation to gridded data in any number of variables.

If, for example, the given data over a three-dimensional grid are contained in some three-dimensional array v of size [Nx,Ny,Nz], with v(i,j,k) containing the value f(x(i), y(j), z(k)), then we would start off with

coefs = reshape(v,Nx,Ny*Nz);

Assuming that nj = knotsj - kj, for j = x,y,z, we would then proceed as follows: 

sp = spap2(knotsx,kx,x,coefs.');
coefs = reshape(fnbrk(sp,'c'),Ny,Nz*nx);
sp = spap2(knotsy,ky,y,coefs.'); 
coefs = reshape(fnbrk(sp,'c'),Nz,nx*ny);
sp = spap2(knotsz,kz,z,coefs.'); 
coefs = reshape(fnbrk(sp,'c'),nx,ny*nz);

See Chapter 17 of PGS or [C. de Boor, "Efficient computer manipulation of tensor products", ACM Trans. Math. Software 5 (1979), 173-182; Corrigenda, 525] for more details. The same references also make clear that there is nothing special here about using least-squares approximation. Any approximation process, including spline interpolation, whose resulting approximation has coefficients that depend linearly on the given data, can be extended in the same way to a multivariate approximation process to gridded data. 

This is exactly what is used, in the spline construction commands csapi, csape, spapi, spaps, and spap2, when gridded data are to be fitted. It is also used, in fnval, when a tensor product spline is to be evaluated on a grid.

Example: Construction of the Chebyshev Spline

Reference