Spline Toolbox

Example: A Nonlinear ODE

The following sample can be run via difeqdem.

We consider the nonlinear singularly perturbed problem

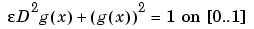
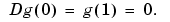
  We seek an approximate solution by collocation from C¹ piecewise cubics with a suitable break sequence; for instance,

breaks = [0:4]/4;

Since cubics are of order 4, we have

k = 4;

and since C¹ requires two smoothness conditions across each interior break, we want knot multiplicity =4-2 =2, hence use the knot sequence   

knots = sort([0 0 breaks breaks 1 1]);

which we could also have obtained as knots = augknt(breaks,4,2). This gives a quadruple knot at both 0 and 1, which is consistent with the fact that we have cubics, i.e., have order 4.

This implies that we have

n = length(knots)-k

= 10 degrees of freedom. We collocate at two sites per polynomial piece, i.e., at eight sites altogether. This, together with the two side conditions, gives us 10 conditions, which matches the 10 degrees of freedom.

We choose the two Gauss sites for each interval. For the standard interval
[-1/2 . . 1/2] of length 1, these are the two sites

gauss = [-1; 1]/(sqrt(3)*2);

From this, we obtain the whole collection of collocation sites by

ninterv = length(breaks)-1; 
temp = ((breaks(2:ninterv+1)+breaks(1:ninterv))/2); 
temp = temp([1 1],:) + gauss*diff(breaks); 
colpnts = temp(:).';

With this, the numerical problem we want to solve is to find 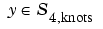that satisfies the nonlinear system

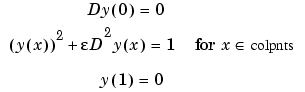
If y is our current approximation to the solution, then the linear problem for the supposedly better solution z by Newton's method reads

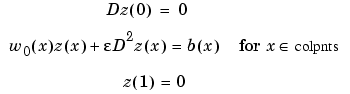
with w₀(x) := 2y(x), b(x) := (y(x))² + 1. In fact, by choosing

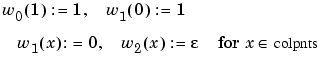
and choosing all other values of not yet specified to be zero, we can give our system the uniform shape

with

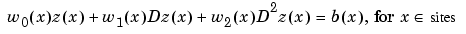
sites = [0,colpnts,1]; 

Since 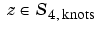, we convert this last system into a system for the B-spline coefficients of z. This requires the values, first, and second derivatives at every 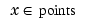and for all the relevant B-splines. The command spcol was expressly written for this purpose.

We use spcol to supply the matrix

colmat = ...
spcol(knots,k,reshape([sites(1 1 1],:),1,(length(sites)));

From this, we get the collocation matrix by combining the row triple of colmat for x using the weights w₀(x), w₁(x), w₂(x) to get the row for x of the actual matrix. For this, we need a current approximation y. Initially, we get it by interpolating some reasonable initial guess from our piecewise-polynomial space at the sites. We use the parabola ()² - 1 (i.e., the function

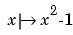) that satisfies the end conditions as the initial guess, and pick the matrix from the full matrix colmat. Here it is, in several cautious steps:

intmat = colmat([2 1+[1:8]*3,1+9*3],:); 
coefs = intmat\[0 colpnts.*colpnts-1 0].'; 
y = spmak(knots,coefs.');

We can now complete the construction and solution of the linear system for the improved approximate solution z from our current guess y. In fact, with the initial guess y available, we now set up an iteration, to be terminated when the change z-y is small enough. We choose a relatively mild .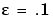

epsilon =.1;
tolerance=1.e-9;
while 1 
  vtau=fnval(y,colpnts); 
  weights = [0 1 0; 
             [2*vtau.'zeros(8,1) epsilon*ones(8,1)]; 
             1 0 0]; 
  colloc = zeros(10,10); 
  for j=1:10 
     colloc(j,:)=weights(j,:)*colmat(3*(j-1)+[1:3],:); 
  end 
  coefs = colloc\[0 vtau.*vtau+1 0].'; 
  z = spmak(knots,coefs.'); 
  maxdif = max(abs(z-y)) 
if maxdif<tolerance, break, end 
    y = z; 
end

The resulting printout of the errors

maxdif = 0.2067 
maxdif = 0.0121 
maxdif = 3.9515e-005 
maxdif = 4.4322e-010

shows the quadratic convergence expected from Newton's method. The plot below shows the initial guess and the computed solution, as the two leftmost curves. Note that the computed solution, like the exact solution, does not equal -1 at 0.

Figure 1-15: Solutions of a Nonlinear ODE with Increasingly Strong Boundary Layer

If we now decrease 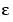, we create more of a boundary layer near the right endpoint, and this calls for a nonuniform mesh.

We use newknt to construct an appropriate finer mesh from the current approximation:

knots = newknt(z, ninterv+1); breaks = knt2brk(knots);
knots = augknt(breaks,4,2); 
n = length(knots)-k;

From the new break sequence, we generate the new collocation site sequence:

ninterv = length(breaks)-1; 
temp = ((breaks(2:ninterv+1)+breaks(1:ninterv))/2); 
temp = temp([1 1], :) + gauss*diff(breaks); 
colpnts = temp(:).'; 
sites = [0,colpnts,1];

We use spcol to supply the matrix

colmat = spcol(knots,k,sort([sites sites sites]));

and use our current approximate solution z as the initial guess:

intmat = colmat([2 1+[1:(n-2)]*3,1+(n-1)*3],:); 
y = spmak(knots,[0 fnval(z,colpnts) 0]/intmat.');

Thus set up, we cut 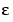by 3 and repeat the earlier calculation, starting with the statements

tolerance=1.e-9; 
while 1 
  vtau=fnval(y,colpnts);
  .
  .
  .

Repeated passes through this process generate a sequence of solutions, for 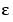= 1/10, 1/30, 1/90, 1/270, 1/810. The resulting solutions, ever flatter at 0 and ever steeper at 1, are shown in the plot above. The plot also shows the final break sequence, as a sequence of vertical bars.

In this example, at least, newknt has performed satisfactorily.

NURBS and Other Rational Splines

Example: Construction of the Chebyshev Spline