Spline Toolbox

Tensor Product Splines

The toolbox provides spline functions in any number of variables, as tensor products of univariate splines. These multivariate splines come in both standard forms, the B-form and the ppform, and their construction and use parallels entirely that of the univariate splines discussed in previous sections. The same commands are used for their construction and use.

For simplicity, the discussion to follow deals just with bivariate splines.

The tensor-product idea is very simple. If f  is a function of x and g is a function of y, then their tensor-product 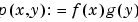is a function of x and y, i.e., a bivariate function. More generally, with 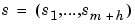and 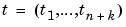knot sequences and

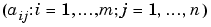a corresponding coefficient array, we obtain a bivariate spline as

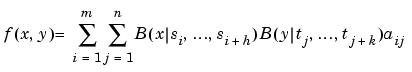
The B-form of this spline comprises the cell array {s,t} of its knot sequences, the coefficient array a, the numbers vector [m,n], and the orders vector [h,k]. The command

sp = spmak({s,t},a);

constructs this form. Further, fnplt, fnval, fnder, fndir, fnrfn, fn2fm can be used to plot, evaluate, differentiate and integrate, refine, and convert this form.

You are most likely to construct such a form by looking for an interpolant or approximant to gridded data. For example, if you know the values z(i,j) = g(x(i), y(j)), i=1:m, j=1:n, of some function g at all the points in a rectangular grid, then, assuming that the strictly increasing sequence x satisfies the Schoenberg-Whitney conditions with respect to the above knot sequence s and that the strictly increasing sequence y satisfies the Schoenberg-Whitney conditions with respect to the above knot sequence t, the command

sp = spapi( {s,t}, [h k], {x,y}, z );

constructs the unique bivariate spline of the above form that matches the given values. The command fnplt(sp) gives you a quick plot of this interpolant. The command pp = fn2fm(sp,'pp') gives you the ppform of this spline which is probably what you want when you want to evaluate the spline at a fine grid ((xx(i),yy(j)) for i=1:M, j=1:N), by the command:

values = fnval(pp,{xx,yy});

The ppform of such a bivariate spline comprises, analogously, a cell array of break sequences, a multidimensional coefficient array, a vector of number pieces, and a vector of polynomial orders. Fortunately, the toolbox is set up in such a way that there is usually no reason for you to concern yourself with these details of either form. You use interpolation, approximation or smoothing to construct splines, and then use the fn... commands to make use of them.

Here is an example of a surface constructed as a 3-D-valued bivariate spline. The surface is the famous Moebius band, obtainable by taking a longish strip of paper and gluing its narrow ends together, but with a twist. The figure is obtained by the following commands:

x = 0:1; y = 0:4; h = 1/4; o2 = 1/sqrt(2); s = 2; ss = 4;
v(3,:,:) = h*[0, -1, -o2, 0, o2, 1, 0;0, 1, o2, 0, -o2, -1, 0];
v(2,:,:) = [ss, 0, s-h*o2, 0, -s-h*o2, 0, ss;...
            ss, 0, s+h*o2, 0,-s+h*o2, 0, ss];
v(1,:,:) = s*[0, 1, 0, -1+h, 0, 1, 0; 0, 1, 0, -1-h, 0, 1, 0];
cs = csape({x,y},v,{'variational','clamped'});
fnplt(cs), axis([-2 2 -2.5 2.5 -.5 .5]), shading interp
axis off, hold on
values = squeeze(fnval(cs,{1,linspace(y(1),y(end),51)}));
plot3(values(1,:), values(2,:), values(3,:),'k','linew',2)
hold off

Figure 1-12: A Moebius Band Made by Vector-Valued Bivariate Spline Interpolation

The B-form

NURBS and Other Rational Splines