

| Robust Control Toolbox |   |
State-space sector bilinear transformation.
[ag,bg1,,dg22,at,bt1,,dt21,dt22] = sectf(af,bf1,,df22,secf,secg) [ag,bg,cg,dg,at,bt1,,dt21,dt22] = sectf(af,bf,cf,df,secf,secg) [tssg,tsst] = sectf(tssf,secf,secg) [ssg,tsst] = sectf(ssf,secf,secg)
Description
sectf may be used to transform conic-sector control system performance specifications into equivalent H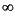 -norm performance specifications. Given a two-port state-space system F(s) := tssf,
-norm performance specifications. Given a two-port state-space system F(s) := tssf, sectf computes a linear-fractionally-transformed two-port state-space system G(s) := tssg such that the channel-one Input-Output (I/O) pairs (ug1, yg1) of G(s) are in sector secg if and only if the corresponding I/O pairs of F(s) are in secf. Also computed is a two-port system T(s) such that G(s) is obtained via the MATLAB command tssg=lftf(tsst,tssf).
A,B are scalars in [-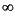 ,
, 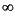 ] or square matrices;
] or square matrices; a,b are vectors; S=[S11 S12;S21,S22] is a square matrix whose blocks S11,S12,S21,S22 are either scalars or square matrices; tsss is a two-port system tsss=mksys(a,b1,b2,,'tss') with transfer function 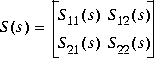 Output variables are:
Output variables are:
Here tssf, tsst, and tssg are two-port state-space representations of F(s), T(s), and G(s).
If the input F(s) is specified as a standard state-space system ssf, then the sector transformation is performed on all channels of F(s), so that the output G(s) will likewise be returned in standard state-space form ssg.
Examples
The statement G(j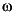 ) inside sector[-1, 1] is equivalent to the H
) inside sector[-1, 1] is equivalent to the H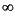 inequality
inequality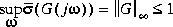
tssp1 = sectf(tssp,[0,Inf],[-1,1]) computes a transformed P(s) := tssp1 such that an H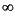 feedback K(s), which places the closed-loop transformed system inside sector[-1, 1], also places the original system inside sector[0,
feedback K(s), which places the closed-loop transformed system inside sector[-1, 1], also places the original system inside sector[0, 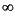 ]. See Figure 1-14.
]. See Figure 1-14.
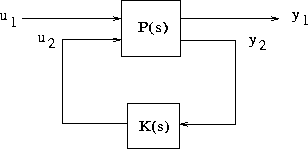
Figure 1-14: Sector Transform Block Diagram.
Here is a simple example of the sector transform.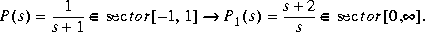 You can compute this by simply executing the following commands:
You can compute this by simply executing the following commands:
[A,B,C,D] = tf2ss(1,[1 1]); [a,b,c,d] = sectf(A,B,C,D,[-1,1],[0,Inf]);The Nyquist plots for this transformation are depicted in Figure 1-15. The condition P1(s) inside [0,
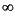 ] implies that P1(s) is stable and P1(j
] implies that P1(s) is stable and P1(j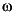 ) is positive real, i.e.,
) is positive real, i.e.,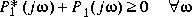
sectf is a M-file in the Robust Control Toolbox that uses the generalization of the sector concept of [3] described by [1]. First the sector input data Sf= secf and Sg=secg is converted to two-port state-space form; non-dynamical sectors are handled with empty a, b1, b2, c1, c2 matrices. Next the equation 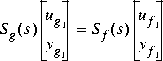 is solved for the two-port transfer function T(s) from
is solved for the two-port transfer function T(s) from 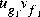 to
to 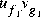 . Finally, the function
. Finally, the function lftf is used to compute G(s) via one of the following:
tssg=lftf(tsst,tssg) ssg=lftf(tsst,ssg).
Figure 1-15: Example of Sector Transform.
Limitations
A well-posed conic sector must have 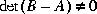 or
or 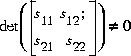 .
.
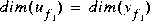 since sectors are only defined for square systems.
since sectors are only defined for square systems.
References
[1] M. G. Safonov, Stability and Robustness of Multivariable Feedback Systems. Cambridge, MA: MIT Press, 1980.
 -- Part I: Conditions Using Concepts of Loop Gain, Conicity, and Positivity," IEEE Trans. on Automat. Contr., AC-11, pp. 228-238, 1966.
-- Part I: Conditions Using Concepts of Loop Gain, Conicity, and Positivity," IEEE Trans. on Automat. Contr., AC-11, pp. 228-238, 1966.
 | riccond | sfl, sfr |  |