

| Robust Control Toolbox |   |
Condition numbers of continuous algebraic Riccati equation.
[tot] = riccond(a,b,qrn,p1,p2)
Description
Riccond provides the condition numbers of continuous Riccati equation. The input variable qrn contains the weighting matrix
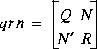
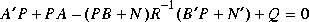 where P = P2/P1 is the positive definite solution of ARE, and [P2; P1] spans the stable eigenspace of the Hamiltonian
where P = P2/P1 is the positive definite solution of ARE, and [P2; P1] spans the stable eigenspace of the Hamiltonian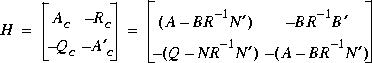 Several measurements are provided:
Several measurements are provided:
norAc, norQc, norRc of matrices Ac, Qc, and Rc, respectively.
conR of R.
conP1 of P1.
conArn) [1].
conBey) [2].
res).
tot puts the above measurements in a column vector
tot= [norA,norQ,norRc,conR,conP1,conBey,res]'For an ill-conditioned problem, one or more of the above measurements could become large. Together, these measurements give a general sense of the Riccati problem conditioning issues.
Algorithm
Arnold and Laub's Riccati condition number is computed as follows [1]:
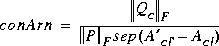
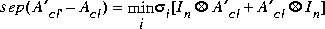 Byers' Riccati condition number is computed as [2]
Byers' Riccati condition number is computed as [2]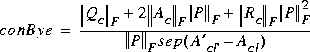
See Also
are, aresolv, daresolv, driccond
References
[1] W. F. Arnold, III and A. Laub, "Generalized Eigenproblem Algorithms and Software for Algebraic Riccati Equations," Proceedings of the IEEE, Vol. 72, No. 12, Dec. 1984.
 | reig | sectf |  |