| Robust Control Toolbox | |
Generalized continuous algebraic Riccati Solver.
[p1,p2,lamp,perr,wellposed,p] = aresolv(a,q,r) [p1,p2,lamp,perr,wellposed,p] = aresolv(a,q,r,Type)
Description
aresolv solves the continuous algebraic Riccati equation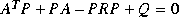 
p=p1/p2 is the solution for which the eigenvalues of A - RP have negative real parts. This solution exists and is unique provided that the associated Hamiltonian matrix has no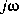 
-axis eigenvalues; otherwise, the flag wellposed is set to the string value 'FALSE'.
Two algorithms are available:
Type = 'eigen' -- eigenvector approach
Type = 'Schur' -- Schur vector approach
Type 'eigen' is selected by default, when the input argument Type is missing, provided that the associated Hamiltonian matrix is not defective (i.e., does not have a full set eigenvectors); otherwise the algorithm defaults to Type 'Schur'. If Type = 'Schur', then the Schur approach is taken directly.
The residual and closed loop eigenvalues are also returned in variables perr and lamp.
In game theory and H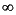
applications, the weighting matrix R is usually indefinite. The program is coded to permit such cases.
Algorithm
The eigenvector approach (Type = 'eigen') uses reig to find a real basis V1 for the stable eigenspace of the Hamiltonian H [1]
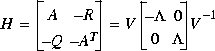
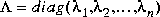and
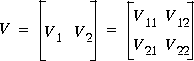The first n columns (V1) of the matrix V that form the stable eigenspace of H also provide the desired solution of ARE:
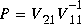where V21 = p2 and V11 = p1 respectively. This algorithm requires about 120n3 flops.
The eigenvector approach can be numerically unstable when the Hamiltonian matrix is close to defective, as can occur some cases in which H is close to a matrix whose Jordan form has ones above its main diagonal. In this case, the matrix V11 will be ill-conditioned. However, the ill-conditioning of V11 is independent of the conditioning of the Riccati equation (ref. riccond, where six types of Riccati condition numbers are provided).
To circumvent the ill-conditioning problems associated with a defective Hamiltonian matrix, you can span the same stable eigenspace of Hamiltonian with Schur vectors [2]. In this approach the Hamiltonian H is orthogonally transformed into the ordered Schur form instead of modal form: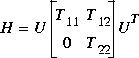
where eigenvalues of T11 are stable and those of T22 are unstable.
The orthogonal matrix U can be partitioned as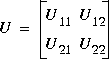 
where the first n column vectors span the same stable eigenspace as V1 matrix. It is proved in [2] that the desired solution of ARE is 
.
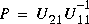The Schur algorithm coded in aresolv first puts H in the ordered complex Schur form using cschur, then projects the complex basis into a real basis using the QR algorithm. The entire ordered Schur method takes about 75n3 flops, which is less than the eigenvector approach.
However, the Schur method itself can also become numerically unstable, if the norm of certain matrices involved in the Riccati equation are much smaller than the norms of others [3]. Our experience has been that more often than not, the eigenvector method performs more reliably than the Schur method, with the notable exception of the case of a defective Hamiltonian mentioned above. In difficult cases in which both eigenvector and Schur methods produce a large residual error, Newton methods may be used to refine the result.
If A is stable, and weighting matrix Q is zero, P2 = 0 and P1 = I are returned without going through the eigenspace computations.
If the sixth output P is not included, aresolv ignores its computation as well. This can avoid some possible singular cases occurring in computing the "optimal" H controller. If P1 is singular or nearly so, the rank deficient P1 matrix will be used to form the H controller, but the null space of the descriptor is removed by des2ss at the final stage of the computation (see the reference pages des2ss and hinf for details).
Limitations
The Riccati equation is ill-posed if the Hamiltonian H has imaginary axis eigenvalues. In cases in which Q, R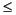 
0, it suffices for the system ((A, R, Q)) to be both stabilizable and detectable to avoid imaginary axis eigenvalues; in this case the unique stabilizing Riccati solution will be positive semidefinite. In any case, the output variable wellposed is returned with the value TRUE or FALSE to reflect the well-posedness of the problem.
See Also
are, cschur, daresolv, lqrc, reig, riccond
References
[1] J. E. Potter, "Matrix Quadratic Solutions," SIAM J. Appl. Math., Vol. 14, pp. 496-501, 1966.
| Reference | augd | |