Tutorial (Power System Blockset)

Power System Blockset

Modeling a Nonlinear Inductance

Let us consider an inductor of 2 henries designed to operate at a nominal voltage Vnom = 120 V rms, and a nominal frequency fnom = 60 Hz. From zero to 120 V rms the inductor has a constant inductance L = 2 H. When voltage exceeds its nominal voltage, the inductor saturates and its inductance is reduced to Lsat = 0.5 H. The nonlinear flux-current characteristic is plotted on Figure 1-20. Flux and current scales are in per units. The nominal voltage and nominal current are chosen as base values for the per-unit system.

Figure 1-20: Flux-Current Characteristic of the Nonlinear Inductance

The current i flowing in the inductor is a nonlinear function of flux linkage 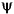which, in turn, is a function of v appearing across its terminals. These relations are given by the equations below:

The model of the nonlinear inductance can therefore be implemented as a controlled current source, where current i is a nonlinear function of voltage v as shown on Figure 1-21.

Figure 1-21: Model of a Nonlinear Inductance

Figure 1-22 shows a PSB circuit using a 2 H nonlinear inductance. The nonlinear inductance is connected in series with two voltage sources (an AC Voltage Source block of 120 Volts rms, 60 Hz and a DC Voltage Source block) and a 5 ohm resistor.

All the elements used to build the nonlinear model have been grouped in a subsystem named Nonlinear Inductance. The inductor terminals are labeled In and Out. Notice that a second output returning the flux has been added to the subsystem. This Simulink output can be used to observe the flux by connecting it to a Simulink Scope block.

The nonlinear model uses two powerlib blocks and two Simulink blocks. The two powerlib blocks are a Voltage Measurement block to read the voltage at the inductance terminals and a Controlled Current Source block. The direction of the arrow of the current source is oriented from input to output according to the model shown on Figure 1-21.

The two Simulink blocks are an Integrator block computing the flux from the voltage input and a Look-Up Table block implementing the saturation characteristic i =f(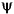) described by Figure 1-20.

Figure 1-22: PSB Implementation of a Nonlinear Inductance

Two Fourier blocks from the Measurements library of powerlib_extras are used to analyze the fundamental component and the DC component of the current.

Using blocks of the powerlib and Simulink libraries, build the circuit of Figure 1-22. To implement the i =f(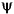) relation, specify the following vectors in the Look-Up Table block:

Vector of input values (flux):[-1.25  -1  1 1.25 ] *(120*sqrt(2)/
(2*pi*60))
Vector of output values (current): [-2 -1 1 2]*(120*sqrt(2)/
(4*pi*60))

Save your circuit as circuit7.

Set the following parameters for the two sources:

AC source:  Peak amplitude = 120*sqrt(2) ; Phase = 90 degrees;
Frequency = 60 Hz
DC source: Amplitude = 0 V

Adjust the simulation time to 1.5 s and select the ode33tb integration algorithm with default parameters. Start the simulation.

As expected, the current and the flux are sinusoidal. Their peak values correspond to the nominal values:

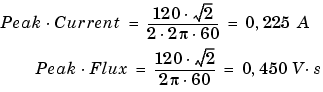
Current and flux waveforms are shown on Figure 1-23.

Figure 1-23: Current and Flux Waveforms Obtained with VDC=0V and
VDC= 1 V

Now change the DC voltage to 1 V and restart the simulation. Observe that the current is distorted. The 1 V DC voltage is now integrated, causing a flux offset, which makes the flux to enter into the nonlinear region of the flux-current characteristic (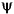 > 0.450 V.s) As a result of this flux saturation, the current contains harmonics. Zoom on the last three cycles of the simulation. The peak value of the current now reaches 0.70 A and the fundamental component has increased to 0.368 A. As expected, the DC component of the current is 1 V/ 0.5 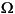= 0.2. The current and flux waveforms obtained with and without saturation are superimposed on Figure 1-23.

Session 7: Building and Customizing Your Own Nonlinear Models Customizing Your Nonlinear Model