

| Power System Blockset |   |
Frequency Analysis
One particular characteristic of series compensated systems is the existence of subsynchronous modes (poles and zeros of the system impedance below the fundamental frequency). Dangerous resonances can occur if the mechanical torsion modes of turbine/generator shafts are in the vicinity of the zeros of the system impedance. Also, high subsynchronous voltages due to impedances poles at subsynchronous frequencies will drive transformers into saturation. The transformer saturation due to subsynchronous voltages is illustrated at the end of this case study. The torque amplification on a thermal machine is illustrated in another demonstration (see psbthermal.mdl file).
Now measure the positive-sequence impedance versus frequency seen from bus B2.
We have already explained in Session 2 of the Tutorial chapter how the Impedance Measurement block allows you to compute the impedance of a linear system from its state-space model. However, your case1 system contains several nonlinear blocks (machine and saturation of transformers). If you connect the Impedance Measurement block to your system, all nonlinear blocks will be ignored. This is correct for the transformer, but you would get the impedance of the system with the machine disconnected. Before measuring the impedance, you must therefore replace the machine block with an equivalent linear block having the same impedance.
Delete the Simplified Synchronous Machine block from your case1 circuit and replace it with the Inductive source with neutral block from the Three-Phase library of powerlib_extras. Open the block dialog box and set the parameters as follows in order to get the same impedance value (L=0.22 pu/ (6*350 MVA) Quality factor=15):
Voltage magnitude (V) :13.8e3/sqrt(3)*sqrt(2)Phase angle : 0Frequency (Hz) : 60Source resistance (Ohms) : 13.8^2/(6*350)*0.22/15Source inductance (H) : 13.8^2/(6*350)*0.22/(2*pi*60)
Save your modified circuit as case1Zf.
Open the Measurements library of powerlib and copy the Impedance Measurement block in your model. This block contains a current source and a voltage measurement that will be used to perform the impedance measurement. Connect the two inputs of this block between phase A and phase B of B2 bus. Measuring the impedance between two phases will give two times the positive-sequence impedance. Therefore you must apply a factor of 1/2 on the impedance in order to obtain the correct impedance value. Open the Impedance Measurement dialog box and set the Multiplication factor to 0.5.
Now open the powergui. In the Tools menu select Impedance vs Frequency Measurement. A new window opens, showing your Impedance Measurement block name. Fill in the frequency range by typing 0:500. Select the linear scales to display Z magnitude vs frequency plot. Check the Save data to workspace button and enter Zcase1 as the variable name that will contain the impedance vs frequency. Click on the Display button.
When the calculation is finished a graphic window appears with the magnitude and phase as a function of frequency. If you check in your workspace, you should have a variable named Zcase1. It is a two-column matrix containing frequency in column 1 and complex impedance in column 2.
The impedance as function of frequency (magnitude and phase) is shown in Figure 2-7.
Figure 2-7: Impedance vs. Frequency Seen From Bus B2
You can observe three main modes: 9 Hz, 175 Hz, and 370 Hz. The 9 Hz mode is mainly due to a parallel resonance of the series capacitor with the shunt inductors. The 175 Hz and 370 Hz modes are due to the 600 km distributed parameter line. These three modes are likely to be excited at fault clearing.
If you zoom on the impedance in the 60 Hz region, you can find the system's short circuit level at bus B2. You should find a value of 58 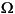 at 60 Hz, corresponding to a three-phase short circuit power of (735kV) 2/58 = 9314 MVA.
at 60 Hz, corresponding to a three-phase short circuit power of (735kV) 2/58 = 9314 MVA.
 | Transient Performance for a Line Fault | Transient Performance for a Fault at Bus B2 |  |