| Partial Differential Equations Toolbox |
  |
assempde
Assemble the stiffness matrix and right-hand side of a PDE problem.
Synopsis
u=assempde(b,p,e,t,c,a,f)
u=assempde(b,p,e,t,c,a,f,u0)
u=assempde(b,p,e,t,c,a,f,u0,time)
u=assempde(b,p,e,t,c,a,f,time)
[K,F]=assempde(b,p,e,t,c,a,f)
[K,F]=assempde(b,p,e,t,c,a,f,u0)
[K,F]=assempde(b,p,e,t,c,a,f,u0,time)
[K,F]=assempde(b,p,e,t,c,a,f,u0,time,sdl)
[K,F]=assempde(b,p,e,t,c,a,f,time)
[K,F]=assempde(b,p,e,t,c,a,f,time,sdl)
[K,F,B,ud]=assempde(b,p,e,t,c,a,f)
[K,F,B,ud]=assempde(b,p,e,t,c,a,f,u0)
[K,F,B,ud]=assempde(b,p,e,t,c,a,f,u0,time)
[K,F,B,ud]=assempde(b,p,e,t,c,a,f,time)
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f)
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f,u0)
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f,u0,time)
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f,u0,time,sdl)
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f,time)
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f,time,sdl)
u=assempde(K,M,F,Q,G,H,R)
[K1,F1]=assempde(K,M,F,Q,G,H,R)
[K1,F1,B,ud]=assempde(K,M,F,Q,G,H,R)
Description
assempde is the basic function of the PDE Toolbox. It assembles a PDE problem by using the FEM formulation described in Chapter 4, "The Finite Element Method". The command assempde assembles the scalar PDE problem
-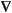 · (c
· (c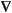 u) + au = f on
u) + au = f on 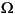 ,
,
or the system PDE problem
-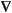 · (c
· (c 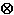
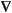 u) + au = f on
u) + au = f on 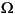 .
.
The command can optionally produce a solution to the PDE problem.
For the scalar case the solution vector u is represented as a column vector of solution values at the corresponding node points from p. For a system of dimension N with np node points, the first np values of u describe the first component of u, the following np values of u describe the second component of u, and so on. Thus, the components of u are placed in the vector u as N blocks of node point values.
u=assempde(b,p,e,t,c,a,f)
assembles and solves the PDE problem by eliminating the Dirichlet boundary conditions from the system of linear equations.
[K,F]=assempde(b,p,e,t,c,a,f)
assembles the PDE problem by approximating the Dirichlet boundary condition with stiff springs (see the section "The Elliptic System" in The Finite Element Method chapter for details). K and F are the stiffness matrix and right-hand side, respectively. The solution to the FEM formulation of the PDE problem is u=K\F.
[K,F,B,ud]=assempde(b,p,e,t,c,a,f)
assembles the PDE problem by eliminating the Dirichlet boundary conditions from the system of linear equations. u1=K\F returns the solution on the non-Dirichlet points. The solution to the full PDE problem can be obtained as the MATLAB expression u=B*u1+ud.
[K,M,F,Q,G,H,R]=assempde(b,p,e,t,c,a,f)
gives a split representation of the PDE problem.
u=assempde(K,M,F,Q,G,H,R)
collapses the split representation into the single matrix/vector form, and then solves the PDE problem by eliminating the Dirichlet boundary conditions from the system of linear equations.
[K1,F1]=assempde(K,M,F,Q,G,H,R)
collapses the split representation into the single matrix/vector form, by fixing the Dirichlet boundary condition with large spring constants.
[K1,F1,B,ud]=assempde(K,M,F,Q,G,H,R)
collapses the split representation into the single matrix/vector form by eliminating the Dirichlet boundary conditions from the system of linear equations.
b
describes the boundary conditions of the PDE problem. b can be either a Boundary Condition matrix or the name of a Boundary M-file. The formats of the Boundary Condition matrix and Boundary M-file are described in the entries on assemb and pdebound, respectively.
The geometry of the PDE problem is given by the mesh data p, e, and t. Details on the mesh data representation can be found in the entry on initmesh.
The optional list of subdomain labels, sdl, restricts the assembly process to the subdomains denoted by the labels in the list. The optional input arguments u0 and time are used for the nonlinear solver and time stepping algorithms, respectively. The tentative input solution vector u0 has the same format as u.
PDE Coefficients for Scalar Case
The coefficients c, a, and f in the scalar PDE problem can be represented in the MATLAB variables c, a, and f in the following ways:
- A constant.
- A row vector of values at the triangle centers of mass.
- A MATLAB text expression for computing coefficient values at the triangle centers of mass. The expression is evaluated in a context where the variables
x, y, sd, u, ux, uy, and t are row vectors representing values at the triangle centers of mass (t is a scalar). The row vectors contain x- and y-coordinates, subdomain label, solution, x and y derivatives of the solution, and time. u, ux, and uy can only be used if u0 has been passed to assempde. The same applies to the scalar t, which is passed to assempde as time.
- A sequence of MATLAB text expressions separated by exclamation marks
!. The syntax of each of the text expressions must be according to the above item. The number of expressions in the sequence must equal the number of subdomain labels in the triangle list t. (This number can be checked by typing max(t(4,:)).)
- The name of a user-defined MATLAB function that accepts the arguments (
p,t,u,time). u and time are empty matrices if the corresponding parameter is not passed to assempde. p and t are mesh data, u is the u0 input argument, and t is the time input argument to assempde. If time is NaN and the function depends on time, the function must return a matrix of correct size, containing NaNs in all positions.
We refer to the matrices above as Coefficient matrix, and the user-defined MATLAB function as Coefficient M-file.
If c contains two rows with data according to any of the above items, they are the c1,1, and c2,2, elements of the 2-by-2 diagonal matrix
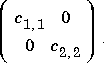 If
If c contains four rows, they are the c1,1, c2,1, c1,2, and c2,2 elements of a 2-by-2 matrix.
PDE Coefficients for System Case
Let N be the dimension of the PDE system. Now c is an N-by-N-by-2-by-2 tensor, a an N-by-N-matrix, and f a column vector of length N. The elements cijkl, aij, dij, and fi of c, a, d, and f are stored row-wise in the MATLAB matrices c, a, d, and f. Each row in these matrices is similar in syntax to the scalar case. There is one difference, however: At the point of evaluation of MATLAB text expressions, the variables u, ux, and uy contain matrices with N rows, one row for each component. The case of identity, diagonal, and symmetric matrices are handled as special cases. For the tensor cijkl this applies both to the indices i and j, and to the indices k and l.
The number of rows in f determines the dimension N of the system. Row i in f represents the component fi in f.
The number of rows na in a is related to the components aij of a according to the following table. For the symmetric case assume that j 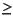 i. All elements aij that cannot be formed are assumed to be zero:
i. All elements aij that cannot be formed are assumed to be zero:
na
|
Symmetric
|
aij
|
Row in a
|
1
|
No
|
aii
|
1
|
N
|
No
|
aii
|
i
|
N(N + 1)/2
|
Yes
|
aij
|
j(j - 1)/2 + i
|
N2
|
No
|
aij
|
N(j - 1) + i
|
An example of how a is stored in a can be found below.
The coding of c in c is determined by the dimension N and the number of rows nc in c. The number of rows nc in c is matched to the function of N in the first column in the table below -- sequentially from the first line to the last line.
The first match determines the type of coding of c. This actually means that for some small values, 2 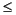 N
N 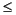 4, the coding is only determined by the order in which the tests are performed. For the symmetric case assume that j
4, the coding is only determined by the order in which the tests are performed. For the symmetric case assume that j 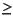 i,
i,
and l 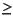 k. All elements cijkl that can not be formed are assumed to be zero:
k. All elements cijkl that can not be formed are assumed to be zero:
nc
|
Symmetric
|
cijkl
|
Row in c
|
1
|
No
|
ciikk
|
1
|
2
|
No
|
ciikk
|
k
|
3
|
Yes
|
ciikl
|
l + k - 1
|
4
|
No
|
ciikl
|
2l + k - 2
|
N
|
No
|
ciikk
|
i
|
2N
|
No
|
ciikk
|
2i + k - 2
|
3N
|
Yes
|
ciikl
|
3i + l + k - 4
|
4N
|
No
|
ciikl
|
4i + 2l + k - 6
|
2N(2N + 1)/2
|
Yes
|
ciikl
|
2j2 + j + l + k - 4
|
|
|
cijkl
|
2j2 - 3j + 4i + 2l + k - 5
|
4N2
|
No
|
cijkl
|
4N(j - 1)+ 4i + 2l + k - 6
|
An example of how c is stored in c can be found below.
Examples
Example 1
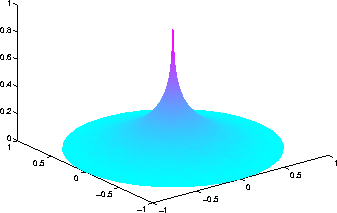
Solve the equation 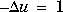 on the geometry defined by the L-shaped membrane. Use Dirichlet boundary conditions u = 0 on
on the geometry defined by the L-shaped membrane. Use Dirichlet boundary conditions u = 0 on 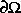 . Finally plot the solution.
. Finally plot the solution.
» [p,e,t]=initmesh('lshapeg','Hmax',0.2);
» [p,e,t]=refinemesh('lshapeg',p,e,t);
» u=assempde('lshapeb',p,e,t,1,0,1);
» pdesurf(p,t,u)
Example 2
Consider Poisson's equation on the unit circle with unit point source at the origin. The exact solution
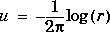
is known for this problem. We define the function f=circlef(p,t,u,time) for computing the right-hand side. circlef returns zero for all triangles except for the one located at the origin; for that triangle it returns 1/a, where a is the triangle area. pdedemo7 performs a full demonstration of the problem with adaptive solution.
 Example 3
Example 3
We study how the matrices a (and also d) are stored in the MATLAB matrix a for system case N = 3:
na = 1:
| a(1)
|
0
|
0
|
na = 3:
| a(1)
|
0
|
0
|
0
|
a(1)
|
0
|
0
|
a(2)
|
0
|
0
|
0
|
a(1)
|
0
|
0
|
a(3)
|
The bullet symbol (·) below means that the matrix is symmetric:
na = 6:
| a(1)
|
a(2)
|
a(4)
|
na = 9:
| a(1)
|
a(4)
|
a(7)
|
·
|
a(3)
|
a(5)
|
a(2)
|
a(5)
|
a(8)
|
·
|
·
|
a(6)
|
a(3)
|
a(6)
|
a(9)
|
We study how the tensor c is stored in the MATLAB matrix c for the system caseN = 3:
nc = 2:
| c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(2)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(2)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(2)
|
nc = 1:
| c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
The bullet symbol (·) below means that the matrix is symmetric:
nc = 3:
| c(1)
|
c(2)
|
0
|
0
|
0
|
0
|
·
|
c(3)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
c(2)
|
0
|
0
|
0
|
0
|
·
|
c(3)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
c(2)
|
0
|
0
|
0
|
0
|
·
|
c(3)
|
nc = 4:
| c(1)
|
c(3)
|
0
|
0
|
0
|
0
|
c(2)
|
c(4)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
c(3)
|
0
|
0
|
0
|
0
|
c(2)
|
c(4)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(1)
|
c(3)
|
0
|
0
|
0
|
0
|
c(2)
|
c(4)
|
The case nc = 3 takes precedence over the case nc = N, and the form nc = N thus cannot be used.
nc = 6:
| c(1)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(2)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(3)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(4)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(5)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(6)
|
nc = 9:
| c(1)
|
c(2)
|
0
|
0
|
0
|
0
|
·
|
c(3)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(4)
|
c(5)
|
0
|
0
|
0
|
0
|
·
|
c(6)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(7)
|
c(8)
|
0
|
0
|
0
|
0
|
·
|
c(9)
|
nc = 12:
| c(1)
|
c(3)
|
0
|
0
|
0
|
0
|
c(2)
|
c(4)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(5)
|
c(7)
|
0
|
0
|
0
|
0
|
c(6)
|
c(8)
|
0
|
0
|
0
|
0
|
0
|
0
|
c(9)
|
c(11)
|
0
|
0
|
0
|
0
|
c(10)
|
c(12)
|
nc = 21:
| c(1)
|
c(2)
|
c(4)
|
c(6)
|
c(11)
|
c(13)
|
·
|
c(3)
|
c(5)
|
c(7)
|
c(12)
|
c(14)
|
·
|
·
|
c(8)
|
c(9)
|
c(15)
|
c(17)
|
·
|
·
|
·
|
c(10)
|
c(16)
|
c(18)
|
·
|
·
|
·
|
·
|
c(19)
|
c(20)
|
·
|
·
|
·
|
·
|
·
|
c(21)
|
nc = 36:
| c(1)
|
c(3)
|
c(13)
|
c(15)
|
c(25)
|
c(27)
|
c(2)
|
c(4)
|
c(14)
|
c(16)
|
c(26)
|
c(28)
|
c(5)
|
c(7)
|
c(17)
|
c(19)
|
c(29)
|
c(31)
|
c(6)
|
c(8)
|
c(18)
|
c(20)
|
c(30)
|
c(32)
|
c(9)
|
c(11)
|
c(21)
|
c(23)
|
c(33)
|
c(35)
|
c(10)
|
c(12)
|
c(22)
|
c(24)
|
c(34)
|
c(36)
|
See Also
initmesh, refinemesh, pdebound, assema, assemb
 | assemb | | csgchk |  |




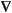 · (c
· (c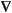 u) + au = f on
u) + au = f on 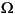 ,
-
,
-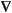 · (c
· (c 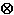
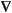 u) + au = f on
u) + au = f on 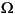 .
.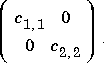 If
If  i. All elements aij that cannot be formed are assumed to be zero:
i. All elements aij that cannot be formed are assumed to be zero: N
N  4, the coding is only determined by the order in which the tests are performed. For the symmetric case assume that j
4, the coding is only determined by the order in which the tests are performed. For the symmetric case assume that j 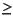 i,
i, 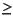 k. All elements cijkl that can not be formed are assumed to be zero:
k. All elements cijkl that can not be formed are assumed to be zero: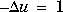 on the geometry defined by the L-shaped membrane. Use Dirichlet boundary conditions u = 0 on
on the geometry defined by the L-shaped membrane. Use Dirichlet boundary conditions u = 0 on 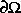 . Finally plot the solution.
. Finally plot the solution.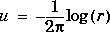
 Example 3
Example 3
