

| Partial Differential Equations Toolbox |   |
[q,g,h,r]=pdebound(p,e,u,time)
Description
The Boundary M-file specifies the boundary conditions of a PDE problem.
By the notation 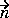 ·(c
·(c 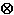
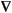 u) we mean the N-by-1 matrix with (i,1)-component
u) we mean the N-by-1 matrix with (i,1)-component
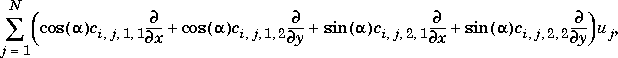
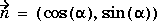 .
There are M Dirichlet conditions and the h-matrix is M-by-N, M
.
There are M Dirichlet conditions and the h-matrix is M-by-N, M 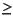 0. The generalized Neumann condition contains a source h'm where the Lagrange multipliers µ is computed such that the Dirichlet conditions become satisfied.
The data that you specify is q, g, h, and r.
For M = 0 we say that we have a generalized Neumann boundary condition, for M = N a Dirichlet boundary condition, and for 0 < M < N a mixed boundary condition.
The Boundary M-file
0. The generalized Neumann condition contains a source h'm where the Lagrange multipliers µ is computed such that the Dirichlet conditions become satisfied.
The data that you specify is q, g, h, and r.
For M = 0 we say that we have a generalized Neumann boundary condition, for M = N a Dirichlet boundary condition, and for 0 < M < N a mixed boundary condition.
The Boundary M-file [q,g,h,r]=pdebound(p,e,u,time) computes the values of q, g, h, and r, on the a set of edges e.
The matrices p and e are mesh data. e needs only to be a subset of the edges in the mesh. Details on the mesh data representation can be found in the entry on initmesh.
The input arguments u and time are used for the nonlinear solver and time stepping algorithms, respectively. u and time are empty matrices if the corresponding parameter is not passed to assemb. If time is NaN and any of the function q, g, h, and r depends on time, pdebound must return a matrix of correct size, containing NaNs in all positions, in the corresponding output argument.
The solution u is represented by the solution vector u. Details on the representation can be found in the entry on assempde.
q and g must contain the value of q and g on the midpoint of each boundary. Thus we have size(q)=[N^2 ne], where N is the dimension of the system, and ne the number of edges in e, and size(g)=[N ne]. For the Dirichlet case, the corresponding values must be zeros.
h and r must contain the values of h and r at the first point on each edge followed by the value at the second point on each edge. Thus we have size(h)=[N^2 2*ne], where N is the dimension of the system, and ne the number of edges in e, and size(r)=[N 2*ne]. When M < N, h and r must be padded with N - M rows of zeros.
The elements of the matrices q and h are stored in column-wise ordering in the MATLAB matrices q and h.
Examples
For the boundary conditions
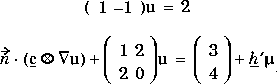
q, g, h, and r:
1
q=[ ... 2 ... ]
2
0
g=[ ... 3 ... ]
4
1 1
h=[ ... 0 ... 0 ... ]
-1 -1
0 0
r=[ ... 2 ... 2 ... ]
0 0
See Also
initmesh, pdegeom, pdesdt, pdeent
 | pdearcl | pdecgrad |  |