Optimization Toolbox

Gauss-Newton Method

In the Gauss-Newton method, a search direction, 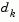, is obtained at each major iteration, k, that is a solution of the linear least squares problem.

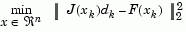
(2-21)

The direction derived from this method is equivalent to the Newton direction when the terms of Q(x) can be ignored. The search direction 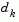can be used as part of a line search strategy to ensure that at each iteration the function f(x) decreases.

To consider the efficiencies that are possible with the Gauss-Newton method. Figure 2-3, Gauss-Newton Method on Rosenbrock's Function, shows the path to the minimum on Rosenbrock's function (Eq. 2-2) when posed as a least squares problem. The Gauss-Newton method converges after only 48 function evaluations using finite difference gradients compared to 140 iterations using an unconstrained BFGS method.

The Gauss-Newton method often encounters problems when the second order term Q(x) in Eq. 2-20 is significant. A method that overcomes this problem is the Levenberg-Marquardt method.

Figure 2-3: Gauss-Newton Method on Rosenbrock's Function

Least Squares Optimization

Levenberg-Marquardt Method