Optimization Toolbox

fminunc

Find the minimum of an unconstrained multivariable function

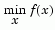
where x is a vector and f(x) is a function that returns a scalar.

Syntax

x = fminunc(fun,x0)
x = fminunc(fun,x0,options)
x = fminunc(fun,x0,options,P1,P2,...)
[x,fval] = fminunc(...)
[x,fval,exitflag] = fminunc(...)
[x,fval,exitflag,output] = fminunc(...)
[x,fval,exitflag,output,grad] = fminunc(...)
[x,fval,exitflag,output,grad,hessian] = fminunc(...)

Description

fminunc finds the minimum of a scalar function of several variables, starting at an initial estimate. This is generally referred to as unconstrained nonlinear optimization.

x = fminunc(fun,x0) starts at the point x0 and finds a local minimum x of the function described in fun. x0 can be a scalar, vector, or matrix.

x = fminunc(fun,x0,options) minimizes with the optimization parameters specified in the structure options.

x = fminunc(fun,x0,options,P1,P2,...) passes the problem-dependent parameters P1, P2, etc., directly to the function fun. Pass an empty matrix for options to use the default values for options.

[x,fval] = fminunc(...) returns in fval the value of the objective function fun at the solution x.

[x,fval,exitflag] = fminunc(...) returns a value exitflag that describes the exit condition.

[x,fval,exitflag,output] = fminunc(...) returns a structure output that contains information about the optimization.

[x,fval,exitflag,output,grad] = fminunc(...) returns in grad the value of the gradient of fun at the solution x.

[x,fval,exitflag,output,grad,hessian] = fminunc(...) returns in hessian the value of the Hessian of the objective function fun at the solution x.

Arguments

Input Arguments.   Table 4-1, Input Arguments, contains general descriptions of arguments passed in to fminunc. This section provides function-specific details for fun and options:

fun	The function to be minimized. fun is a function that accepts a vector x and returns a scalar f, the objective function evaluated at x. The function fun can be specified as a function handle. x = fminunc(@myfun,x0) where myfun is a MATLAB function such as function f = myfun(x) f = ...            % Compute function value at x fun can also be an inline object. x = fminunc(inline('norm(x)^2'),x0); If the gradient of fun can also be computed and options.GradObj is 'on', as set by options = optimset('GradObj','on') then the function fun must return, in the second output argument, the gradient value g, a vector, at x. Note that by checking the value of nargout the function can avoid computing g when fun is called with only one output argument (in the case where the optimization algorithm only needs the value of f but not g). function [f,g] = myfun(x) f = ...            % Compute the function value at x if nargout > 1     % fun called with 2 output arguments    g = ...         % Compute the gradient evaluated at x end
	The gradient is the partial derivatives 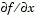of f at the point x. That is, the ith component of g is the partial derivative of f with respect to the ith component of x. If the Hessian matrix can also be computed and options.Hessian is 'on', i.e., options = optimset('Hessian','on'), then the function fun must return the Hessian value H, a symmetric matrix, at x in a third output argument. Note that by checking the value of nargout we can avoid computing H when fun is called with only one or two output arguments (in the case where the optimization algorithm only needs the values of f and g but not H). function [f,g,H] = myfun(x) f = ...     % Compute the objective function value at x if nargout > 1   % fun called with two output arguments    g = ...  % Gradient of the function evaluated at x    if nargout > 2    H = ...  % Hessian evaluated at x end The Hessian matrix is the second partial derivatives matrix of f at the point x. That is, the (i,j)th component of H is the second partial derivative of f with respect to xi and xj, 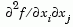. The Hessian is by definition a symmetric matrix.
options	Options provides the function-specific details for the options parameters.

Output Arguments.   Table 4-2, Output Arguments, contains general descriptions of arguments returned by fminunc. This section provides function-specific details for exitflag and output:

exitflag	Describes the exit condition:
	> 0	The function converged to a solution x.
	0	The maximum number of function evaluations or iterations was exceeded.
	< 0	The function did not converge to a solution.
output	Structure containing information about the optimization. The fields of the structure are:
	iterations	Number of iterations taken.
	funcCount	Number of function evaluations.
	algorithm	Algorithm used.
	cgiterations	Number of PCG iterations (large-scale algorithm only).
	stepsize	Final step size taken (medium-scale algorithm only).
	firstorderopt	Measure of first-order optimality: the norm of the gradient at the solution x.

Options

fminunc uses these optimization parameters. Some parameters apply to all algorithms, some are only relevant when using the large-scale algorithm, and others are only relevant when using the medium-scale algorithm.You can use optimset to set or change the values of these fields in the parameters structure, options. See Table 4-3, Optimization Options Parameters,, for detailed information.

We start by describing the LargeScale option since it states a preference for which algorithm to use. It is only a preference since certain conditions must be met to use the large-scale algorithm. For fminunc, the gradient must be provided (see the description of fun above to see how) or else the minimum-scale algorithm is used:

LargeScale

Use large-scale algorithm if possible when set to 'on'. Use medium-scale algorithm when set to 'off'.

Large-Scale and Medium-Scale Algorithms.   These parameters are used by both the large-scale and medium-scale algorithms:

Diagnostics	Print diagnostic information about the function to be minimized.
Display	Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output.
GradObj	Gradient for the objective function defined by user. See the description of fun above to see how to define the gradient in fun. The gradient must be provided to use the large-scale method. It is optional for the medium-scale method.
MaxFunEvals	Maximum number of function evaluations allowed.
MaxIter	Maximum number of iterations allowed.
TolFun	Termination tolerance on the function value.
TolX	Termination tolerance on x.

Large-Scale Algorithm Only.   These parameters are used only by the large-scale algorithm:

Hessian	If 'on', fminunc uses a user-defined Hessian (defined in fun), or Hessian information (when using HessMult), for the objective function. If 'off', fminunc approximates the Hessian using finite differences.
HessMult	Function handle for Hessian multiply function. For large-scale structured problems, this function computes the Hessian matrix product H*Y without actually forming H. The function is of the form W = hmfun(Hinfo,Y,p1,p2,...) where Hinfo and the additional parameters p1,p2,... contain the matrices used to compute H*Y. The first argument must be the same as the third argument returned by the objective function fun. [f,g,Hinfo] = fun(x,p1,p2,...)
	The parameters p1,p2,... are the same additional parameters that are passed to fminunc (and to fun). fminunc(fun,...,options,p1,p2,...) Y is a matrix that has the same number of rows as there are dimensions in the problem. W = H*Y although H is not formed explicitly. fminunc uses Hinfo to compute the preconditioner. Note    'Hessian' must be set to 'on' for Hinfo to be passed from fun to hmfun. See Nonlinear Minimization with a Dense but Structured Hessian and Equality Constraints for an example.
HessPattern	Sparsity pattern of the Hessian for finite-differencing. If it is not convenient to compute the sparse Hessian matrix H in fun, the large-scale method in fminunc can approximate H via sparse finite-differences (of the gradient) provided the sparsity structure of H -- i.e., locations of the nonzeros -- is supplied as the value for HessPattern. In the worst case, if the structure is unknown, you can set HessPattern to be a dense matrix and a full finite-difference approximation is computed at each iteration (this is the default). This can be very expensive for large problems so it is usually worth the effort to determine the sparsity structure.
MaxPCGIter	Maximum number of PCG (preconditioned conjugate gradient) iterations (see the Algorithm section below).
PrecondBandWidth	Upper bandwidth of preconditioner for PCG. By default, diagonal preconditioning is used (upper bandwidth of 0). For some problems, increasing the bandwidth reduces the number of PCG iterations.
TolPCG	Termination tolerance on the PCG iteration.
TypicalX	Typical x values.

Medium-Scale Algorithm Only.   These parameters are used only by the medium-scale algorithm:

DerivativeCheck	Compare user-supplied derivatives (gradient) to finite-differencing derivatives.
DiffMaxChange	Maximum change in variables for finite-difference gradients.
DiffMinChange	Minimum change in variables for finite-difference gradients.
LineSearchType	Line search algorithm choice.

Examples

Minimize the function f(x) = 3*x₁² + 2*x1*x2 + x₂².

To use an M-file, create a file myfun.m.

function f = myfun(x)
f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2;    % Cost function

Then call fminunc to find a minimum of myfun near [1,1].

x0 = [1,1];
[x,fval] = fminunc(@myfun,x0)

After a couple of iterations, the solution, x, and the value of the function at x, fval, are returned.

x =
  1.0e-008 *
   -0.7914    0.2260
fval =
  1.5722e-016

To minimize this function with the gradient provided, modify the M-file myfun.m so the gradient is the second output argument

function [f,g] = myfun(x)
f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2;    % Cost function
if nargout > 1
   g(1) = 6*x(1)+2*x(2);
   g(2) = 2*x(1)+2*x(2);
end

and indicate the gradient value is available by creating an optimization options structure with options.GradObj set to 'on' using optimset.

options = optimset('GradObj','on');
x0 = [1,1];
[x,fval] = fminunc(@myfun,x0,options)

After several iterations the solution x and fval, the value of the function at x, are returned.

x =
  1.0e-015 *
   -0.6661         0
fval2 =
  1.3312e-030

To minimize the function f(x) = sin(x) + 3 using an inline object

f = inline('sin(x)+3');
x = fminunc(f,4)

which returns a solution

x =
    4.7124

Notes

fminunc is not the preferred choice for solving problems that are sums-of-squares, that is, of the form

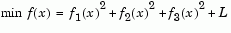
Instead use the lsqnonlin function, which has been optimized for problems of this form.

To use the large-scale method, the gradient must be provided in fun (and options.GradObj set to 'on'). A warning is given if no gradient is provided and options.LargeScale is not 'off'.

Algorithms

Large-Scale Optimization.   By default fminunc chooses the large-scale algorithm if the user supplies the gradient in fun (and GradObj is 'on' in options). This algorithm is a subspace trust region method and is based on the interior-reflective Newton method described in [2],[3]. Each iteration involves the approximate solution of a large linear system using the method of preconditioned conjugate gradients (PCG). See Trust Region Methods for Nonlinear Minimization, and Preconditioned Conjugate Gradients in the "Large-Scale Algorithms" section.

Medium-Scale Optimization.   fminunc with options.LargeScale set to 'off' uses the BFGS Quasi-Newton method with a mixed quadratic and cubic line search procedure. This quasi-Newton method uses the BFGS ([1],[5],[8],[9]) formula for updating the approximation of the Hessian matrix. The DFP ([4],[6],[7]) formula, which approximates the inverse Hessian matrix, is selected by setting options. HessUpdate to 'dfp' (and options.LargeScale to 'off'). A steepest descent method is selected by setting options.HessUpdate to 'steepdesc' (and options.LargeScale to 'off'), although this is not recommended.

The default line search algorithm, i.e., when options.LineSearchType is set to 'quadcubic', is a safeguarded mixed quadratic and cubic polynomial interpolation and extrapolation method. A safeguarded cubic polynomial method can be selected by setting options.LineSearchType to 'cubicpoly'. This second method generally requires fewer function evaluations but more gradient evaluations. Thus, if gradients are being supplied and can be calculated inexpensively, the cubic polynomial line search method is preferable. A full description of the algorithms is given in Standard Algorithms.

Limitations

The function to be minimized must be continuous.fminunc may only give local solutions.

fminunc only minimizes over the real numbers, that is, x must only consist of real numbers and f(x) must only return real numbers. When x has complex variables, they must be split into real and imaginary parts.

Large-Scale Optimization.   To use the large-scale algorithm, the user must supply the gradient in fun (and GradObj must be set 'on' in options). See Table 1-4, Large-Scale Problem Coverage and Requirements for more information on what problem formulations are covered and what information must be provided.

Currently, if the analytical gradient is provided in fun, the options parameter DerivativeCheck cannot be used with the large-scale method to compare the analytic gradient to the finite-difference gradient. Instead, use the medium-scale method to check the derivative with options parameter MaxIter set to 0 iterations. Then run the problem again with the large-scale method.

See Also

@ (function_handle), fminsearch, inline, optimset

References

[1]  Broyden, C.G., "The Convergence of a Class of Double-Rank Minimization Algorithms," Journal Inst. Math. Applic., Vol. 6, pp. 76-90, 1970.

[2]  Coleman, T.F. and Y. Li, "An Interior, Trust Region Approach for Nonlinear Minimization Subject to Bounds," SIAM Journal on Optimization, Vol. 6, pp. 418-445, 1996.

[3]  Coleman, T.F. and Y. Li, "On the Convergence of Reflective Newton Methods for Large-Scale Nonlinear Minimization Subject to Bounds," Mathematical Programming, Vol. 67, Number 2, pp. 189-224, 1994.

[4]  Davidon, W.C., "Variable Metric Method for Minimization," A.E.C. Research and Development Report, ANL-5990, 1959.

[5]  Fletcher, R.,"A New Approach to Variable Metric Algorithms," Computer Journal, Vol. 13, pp. 317-322, 1970.

[6]  Fletcher, R., "Practical Methods of Optimization," Vol. 1, Unconstrained Optimization, John Wiley and Sons, 1980.

[7]  Fletcher, R. and M.J.D. Powell, "A Rapidly Convergent Descent Method for Minimization," Computer Journal, Vol. 6, pp. 163-168, 1963.

[8]  Goldfarb, D., "A Family of Variable Metric Updates Derived by Variational Means," Mathematics of Computing, Vol. 24, pp. 23-26, 1970.

[9]  Shanno, D.F., "Conditioning of Quasi-Newton Methods for Function Minimization," Mathematics of Computing, Vol. 24, pp. 647-656, 1970.

fminsearch

fseminf