

| Optimization Toolbox |   |
Trust Region Methods for Nonlinear Minimization
Many of the methods used in the Optimization Toolbox are based on the trust region idea, a simple yet powerful concept in optimization.
To understand the trust region approach to optimization, consider the unconstrained minimization problem, minimize 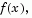 where the function takes vector arguments and returns scalars. Suppose we are at a point
where the function takes vector arguments and returns scalars. Suppose we are at a point 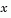 in n-space and we want to improve, i.e., move to a point with a lower function value. The basic idea is to approximate
in n-space and we want to improve, i.e., move to a point with a lower function value. The basic idea is to approximate 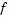 with a simpler function
with a simpler function 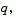 which reasonably reflects the behavior of function
which reasonably reflects the behavior of function 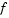 in a neighborhood
in a neighborhood 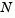 around the point x. This neighborhood is the trust region. A trial step
around the point x. This neighborhood is the trust region. A trial step 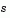 is computed by minimizing (or approximately minimizing) over N. This is the trust region subproblem,
is computed by minimizing (or approximately minimizing) over N. This is the trust region subproblem,
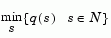
|
(3-1) |
The current point is updated to be 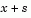 if
if 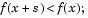 otherwise, the current point remains unchanged and N, the region of trust, is shrunk and the trial step computation is repeated.
otherwise, the current point remains unchanged and N, the region of trust, is shrunk and the trial step computation is repeated.
The key questions in defining a specific trust region approach to minimizing 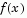 are how to choose and compute the approximation
are how to choose and compute the approximation 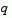 (defined at the current point
(defined at the current point 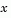 ), how to choose and modify the trust region N, and how accurately to solve the trust region subproblem. In this section we focus on the unconstrained problem; additional complications due to the presence of constraints on the variables are discussed in later sections.
), how to choose and modify the trust region N, and how accurately to solve the trust region subproblem. In this section we focus on the unconstrained problem; additional complications due to the presence of constraints on the variables are discussed in later sections.
In the standard trust region method ([8]), the quadratic approximation 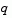 is defined by the first two terms of the Taylor approximation to
is defined by the first two terms of the Taylor approximation to 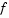 at x; the neighborhood
at x; the neighborhood 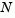 is usually spherical or ellipsoidal in shape. Mathematically the trust region subproblem is typically stated
is usually spherical or ellipsoidal in shape. Mathematically the trust region subproblem is typically stated
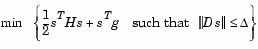
|
(3-2) |
where 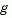 is the gradient of
is the gradient of 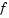 at the current point x,
at the current point x, 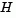 is the Hessian matrix (the symmetric matrix of second derivatives),
is the Hessian matrix (the symmetric matrix of second derivatives), 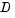 is a diagonal scaling matrix,
is a diagonal scaling matrix, 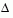 is a positive scalar, and || . || is the 2-norm. Good algorithms exist for solving Eq. 3-2 (see [8]); such algorithms typically involve the computation of a full eigensystem and a Newton process applied to the secular equation
is a positive scalar, and || . || is the 2-norm. Good algorithms exist for solving Eq. 3-2 (see [8]); such algorithms typically involve the computation of a full eigensystem and a Newton process applied to the secular equation
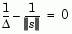
Such algorithms provide an accurate solution to Eq. 3-2, however they require time proportional to several factorizations of H; therefore, for large-scale problems a different approach is needed. Several approximation and heuristic strategies, based on Eq. 3-2, have been proposed in the literature ([2],[10]). The approximation approach we follow in the Optimization Toolbox is to restrict the trust region subproblem to a two-dimensional subspace 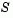 ([1],[2]). Once the subspace
([1],[2]). Once the subspace 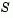 has been computed, the work to solve Eq. 3-2 is trivial even if full eigenvalue/eigenvector information is needed (since in the subspace, the problem is only two-dimensional). The dominant work has now shifted to the determination of the subspace.
has been computed, the work to solve Eq. 3-2 is trivial even if full eigenvalue/eigenvector information is needed (since in the subspace, the problem is only two-dimensional). The dominant work has now shifted to the determination of the subspace.
The two-dimensional subspace 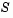 is determined with the aid of a preconditioned conjugate gradient process described below. The toolbox assigns
is determined with the aid of a preconditioned conjugate gradient process described below. The toolbox assigns 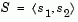 where
where 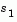 is in the direction of the gradient g, and
is in the direction of the gradient g, and 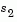 is either an approximate Newton direction, i.e., a solution to
is either an approximate Newton direction, i.e., a solution to
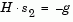
|
(3-3) |
or a direction of negative curvature
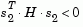
|
(3-4) |
The philosophy behind this choice of 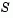 is to force global convergence (via the steepest descent direction or negative curvature direction) and achieve fast local convergence (via the Newton step, when it exists).
is to force global convergence (via the steepest descent direction or negative curvature direction) and achieve fast local convergence (via the Newton step, when it exists).
A framework for the Optimization Toolbox approach to unconstrained minimization using trust region ideas is now easy to describe:
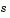
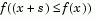 then
then 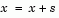
These four steps are repeated until convergence. The trust region dimension 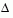 is adjusted according to standard rules. In particular, it is decreased if the trial step is not accepted, i.e.,
is adjusted according to standard rules. In particular, it is decreased if the trial step is not accepted, i.e., 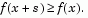 See [6],[9] for a discussion of this aspect.
See [6],[9] for a discussion of this aspect.
The Optimization Toolbox treats a few important special cases of f with specialized functions: nonlinear least squares, quadratic functions, and linear least squares. However, the underlying algorithmic ideas are the same as for the general case. These special cases are discussed in later sections.
 | Large-Scale Algorithms | Preconditioned Conjugate Gradients |  |