

| DSP Blockset |   |
Reconstruct a signal from its multirate bandlimited components (requires the Wavelet Toolbox).
Library
Filtering / Multirate Filters
Description
The Wavelet Synthesis block uses the wfilters function from the Wavelet Toolbox to reconstruct a signal that was decomposed by the Wavelet Analysis block. The reconstruction or synthesis process is the inverse of the analysis process, and restores the original signal by upsampling, filtering, and summing the bandlimited inputs in stages corresponding to the analysis process. An n-level synthesis filter bank structure is shown below, where n is specified by the Number of levels parameter.
At each level, the two bandlimited inputs (one low-frequency, one high-frequency, both with the same sample rate) are upsampled by a factor of 2 to match the sample rate of the input to the next stage. They are then filtered by a highpass (HP) and lowpass (LP) filter pair with coefficients calculated to cancel (in the subsequent summation) the aliasing introduced in the corresponding analysis filter stage. The output from each (upsample-filter-sum) level has twice the bandwidth and twice the sample rate of the input to that level.
For perfect reconstruction, the Wavelet Synthesis and Wavelet Analysis blocks must have the same parameter settings.
Filter Coefficients
The filter coefficients for the highpass and lowpass filters are computed by the Wavelet Toolbox function wfilters, based on the wavelet specified in the Wavelet name parameter. The table below lists the available options.
The Daubechies, Symlets, and Coiflets options enable a secondary Wavelet order parameter that allows you to specify the wavelet order. For example, if you specify a Daubechies wavelet with Wavelet order equal to 6, the Wavelet Synthesis block calls the wfilters function with input argument 'db6'.
The Biorthogonal and Reverse Biorthogonal options enable a secondary Filter order [synthesis / analysis] parameter that allows you to independently specify the wavelet order for the analysis and synthesis filter stages. For example, if you specify a Biorthogonal wavelet with Filter order [synthesis / analysis] equal to [2 / 6], the Wavelet Synthesis block calls the wfilters function with input argument 'bior2.6'.
See the Wavelet Toolbox documentation for more information about the wfilters function. If you want to explicitly specify the FIR coefficients for the synthesis filter bank, use the Dyadic Synthesis Filter Bank block.
Tree Structure
The wavelet tree structure has n+1 inputs, where n is the number of levels. The sample rate and bandwidth of the output are twice the sample rate and bandwidth of the top input. The sample rate and bandwidth of each additional input (except the last) are half that of the input to the previous level.
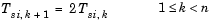
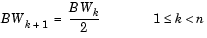
The bottom two inputs (un and un+1) should have the same sample rate and bandwidth since they are processed by the same level.
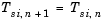
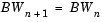
Note that in frame-based mode, the sample period of input uk is reflected by its frame size, Mi,k, rather than by its frame rate.
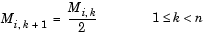
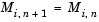
Sample-Based Operation
An M-by-N sample-based matrix input is treated as M*N independent channels, and the block filters each channel independently over time. The output is the same size as the input at each port, one output channel for each input channel. As described earlier, each input port has a different sample period.
The figure below shows the input and output sample periods for the four 64-channel sample-based inputs to a three-level filter bank. The fastest input has a period of 2, so the output period is 1.
Frame-Based Operation
An Mi-by-N frame-based matrix input is treated as N independent channels, and the block filters each channel independently over time. The number of columns in the output is the same as the number of columns in the input.
All inputs must have the same frame period, which is also the output frame period. The different input sample rates should be represented by the input frame sizes: If the input to the top port has frame size Mi, the input to the second-from-top port should have frame size Mi/2, the input to the third-from-top port should have frame size Mi/4, and so on. The input to the bottom port should have the same frame size as the second-from-bottom port. The increase in the sample rate of the output is also represented by its frame size, which is twice the largest input frame size.
The relationship between sample periods, frame periods, and frame sizes is shown below for a four-channel frame-based input to a 3-level filter bank.
Latency
Zero Latency. The Wavelet Synthesis block has no tasking latency for frame-based operation, which is always single-rate. The block therefore uses the first input samples (received at t=0) to synthesize the first output sample.
Nonzero Latency. For sample-based operation, the Wavelet Synthesis block is multirate and has the following tasking latencies:
In the above cases, the block repeats a zero initial condition in each channel for the first D output samples, where D is the latency shown above. For example, in single-tasking mode the block generates 2n-2 zero-valued output samples in each channel before propagating the first synthesized output sample (computed from the inputs received at t=0).
See Excess Algorithmic Delay (Tasking Latency) and "The Simulation Parameters Dialog Box" in the Simulink documentation for more information about block rates and Simulink's tasking modes.
Dialog Box
The parameters displayed in the dialog box vary for different wavelet types. Only some of the parameters listed below are visible in the dialog box at any one time.
[2 / 6] selects a second-order synthesis stage and a sixth-order analysis stage. The Filter order parameter is available only when one of the above wavelets is selected in the Wavelet name menu.References
Fliege, N. J. Multirate Digital Signal Processing: Multirate Systems, Filter Banks, Wavelets. West Sussex, England: John Wiley & Sons, 1994.
Strang, G. and T. Nguyen. Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.
Vaidyanathan, P. P. Multirate Systems and Filter Banks. Englewood Cliffs, NJ: Prentice Hall, 1993.
See Also
| Dyadic Synthesis Filter Bank |
DSP Blockset |
| Wavelet Analysis |
DSP Blockset |
| wfilters |
Wavelet Toolbox |
See the following sections for related information:
 | Wavelet Analysis | Window Function |  |