

| DSP Blockset |   |
Decompose a signal into components of logarithmically decreasing frequency intervals and sample rates (requires the Wavelet Toolbox).
Library
Filtering / Multirate Filters
Description
The Wavelet Analysis block uses the wfilters function from the Wavelet Toolbox to construct a dyadic analysis filter bank that decomposes a broadband signal into a collection of successively more bandlimited components. An n-level filter bank structure is shown below, where n is specified by the Number of levels parameter.
At each level, the low-frequency output of the previous level is decomposed into adjacent high- and low-frequency subbands by a highpass (HP) and lowpass (LP) filter pair. Each of the two output subbands is half the bandwidth of the input to that level. The bandlimited output of each filter is maximally decimated by a factor of 2 to preserve the bit rate of the original signal.
Filter Coefficients
The filter coefficients for the highpass and lowpass filters are computed by the Wavelet Toolbox function wfilters, based on the wavelet specified in the Wavelet name parameter. The table below lists the available options.
The Daubechies, Symlets, and Coiflets options enable a secondary Wavelet order parameter that allows you to specify the wavelet order. For example, if you specify a Daubechies wavelet with Wavelet order equal to 6, the Wavelet Analysis block calls the wfilters function with input argument 'db6'.
The Biorthogonal and Reverse Biorthogonal options enable a secondary Filter order [synthesis / analysis] parameter that allows you to independently specify the wavelet order for the analysis and synthesis filter stages. For example, if you specify a Biorthogonal wavelet with Filter order [synthesis / analysis] equal to [2 / 6], the Wavelet Analysis block calls the wfilters function with input argument 'bior2.6'.
See the Wavelet Toolbox decantation for more information about the wfilters function. If you want to explicitly specify the FIR coefficients for the analysis filter bank, use the Dyadic Analysis Filter Bank block.
Tree Structure
The wavelet tree structure has n+1 outputs, where n is the number of levels. The sample rate and bandwidth of the top output are half the input sample rate and bandwidth. The sample rate and bandwidth of each additional output (except the last) are half that of the output from the previous level. In general, for an input with sample period Tsi = Ts, and bandwidth BW, output yk has sample period Tso,k and bandwidth BWk.
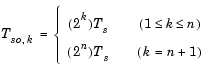
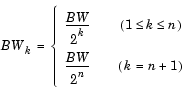
Note that in frame-based mode, the change in the sample period of output yk is reflected by its frame size, Mo,k, rather than by its frame rate.
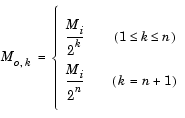
The bottom two outputs (yn and yn+1) share the same sample period, bandwidth, and frame size because they originate at the same tree level.
Sample-Based Operation
An M-by-N sample-based matrix input is treated as M*N independent channels, and the block filters each channel independently over time. The output at each port is the same size as the input, one output channel for each input channel. As described earlier, each output port has a different sample period.
The figure below shows the input and output sample periods for a 64-channel sample-based input to a three-level filter bank. The input has a period of 1, so the fastest output has a period of 2.
Frame-Based Operation
An Mi-by-N frame-based matrix input is treated as N independent channels, and the block filters each channel independently over time. The input frame size Mi must be a multiple of 2n, and n is the number of filter bank levels. For example, a frame size of 8 would be appropriate for a three-level tree (23=8). The number of columns in each output is the same as the number of columns in the input.
Each output port has the same frame period as the input. The reduction in the output sample rates results from the smaller output frame sizes, as shown in the example below for a four-channel input to a three-level filter bank.
Latency
Zero Latency. The Wavelet Analysis block has no tasking latency for frame-based operation, which is always single-rate. The block therefore analyzes the first input sample (received at t=0) to produce the first output sample at each port.
Nonzero Latency. For sample-based operation, the Wavelet Analysis block is multirate and has 2n-1 samples of latency in both Simulink tasking modes. As a result, the block repeats a zero initial condition in each channel for the first 2n-1 output samples, before propagating the first analyzed input sample (computed from the input received at t=0).
See Excess Algorithmic Delay (Tasking Latency) and "The Simulation Parameters Dialog Box" in the Simulink documentation for more information about block rates and Simulink's tasking modes.
Dialog Box
The parameters displayed in the dialog box vary for different wavelet types. Only some of the parameters listed below are visible in the dialog box at any one time.
[2 / 6] selects a second-order synthesis stage and a sixth-order analysis stage. The Filter order parameter is available only when one of the above wavelets is selected in the Wavelet name menu.References
Fliege, N. J. Multirate Digital Signal Processing: Multirate Systems, Filter Banks, Wavelets. West Sussex, England: John Wiley & Sons, 1994.
Strang, G. and T. Nguyen. Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.
Vaidyanathan, P. P. Multirate Systems and Filter Banks. Englewood Cliffs, NJ: Prentice Hall, 1993.
See Also
| Dyadic Analysis Filter Bank |
DSP Blockset |
| Wavelet Synthesis |
DSP Blockset |
| wfilters |
Wavelet Toolbox |
See the following sections for related information:
 | Vector Scope | Wavelet Synthesis |  |