bicg (MATLAB Function Reference)

BiConjugate Gradients method

Syntax

x = bicg(A,b)
bicg(A,b,tol)
bicg(A,b,tol,maxit)
bicg(A,b,tol,maxit,M)
bicg(A,b,tol,maxit,M1,M2)
bicg(A,b,tol,maxit,M1,M2,x0)
bicg(afun,b,tol,maxit,mfun1,mfun2,x0,p1,p2,...)
[x,flag] = bicg(A,b,...)
[x,flag,relres] = bicg(A,b,...)
[x,flag,relres,iter] = bicg(A,b,...)
[x,flag,relres,iter,resvec] = bicg(A,b,...)

Description

x = bicg(A,b) attempts to solve the system of linear equations A*x = b for x. The n-by-n coefficient matrix A must be square and the column vector b must have length n. A can be a function afun such that afun(x) returns A*x and afun(x,'transp') returns A'*x.

If bicg converges, a message to that effect is displayed. If bicg fails to converge after the maximum number of iterations or halts for any reason, a warning message is printed displaying the relative residual norm(b-A*x)/norm(b) and the iteration number at which the method stopped or failed.

bicg(A,b,tol specifies the tolerance of the method. If tol is [], then bicg uses the default, 1e-6.

bicg(A,b,tol,maxit) specifies the maximum number of iterations. If maxit is [], then bicg uses the default, min(n,20).

bicg(A,b,tol,maxit,M) and bicg(A,b,tol,maxit,M1,M2) use the preconditioner M or M = M1*M2 and effectively solve the system inv(M)*A*x = inv(M)*b for x. If M is [] then bicg applies no preconditioner. M can be a function mfun such that mfun(x) returns M\x and mfun(x,'transp') returns M'\x.

bicg(A,b,tol,maxit,M1,M2,x0) specifies the initial guess. If x0 is [], then bicg uses the default, an all-zero vector.

bicg(afun,b,tol,maxit,m1fun,m2fun,x0,p1,p2,...) passes parameters p1,p2,... to functions afun(x,p1,p2,...) and afun(x,p1,p2,...,'transp'), and similarly to the preconditioner functions m1fun and m2fun.

[x,flag] = bicg(A,b,...) also returns a convergence flag.

Flag
Convergence

0
bicg converged to the desired tolerance tol within maxit iterations.

1
bicg iterated maxit times but did not converge.

2
Preconditioner M was ill-conditioned.

3
bicg stagnated. (Two consecutive iterates were the same.)

4
One of the scalar quantities calculated during bicg became too small or too large to continue computing.

Flag	Convergence
`0`	`bicg` converged to the desired tolerance `tol` within `maxit` iterations.
`1`	`bicg` iterated `maxit` times but did not converge.
`2`	Preconditioner `M` was ill-conditioned.
`3`	`bicg` stagnated. (Two consecutive iterates were the same.)
`4`	One of the scalar quantities calculated during `bicg` became too small or too large to continue computing.

Whenever flag is not 0, the solution x returned is that with minimal norm residual computed over all the iterations. No messages are displayed if the flag output is specified.

[x,flag,relres] = bicg(A,b,...) also returns the relative residual norm(b-A*x)/norm(b). If flag is 0, relres <= tol.

[x,flag,relres,iter] = bicg(A,b,...) also returns the iteration number at which x was computed, where 0 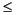iter 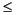maxit.

[x,flag,relres,iter,resvec] = bicg(A,b,...) also returns a vector of the residual norms at each iteration including norm(b-A*x0).

Examples

Example 1.

n = 100; 
on = ones(n,1); 
A = spdiags([-2*on 4*on -on],-1:1,n,n);
b = sum(A,2); 
tol = 1e-8; 
maxit = 15;
M1 = spdiags([on/(-2) on],-1:0,n,n); 
M2 = spdiags([4*on -on],0:1,n,n);

x = bicg(A,b,tol,maxit,M1,M2,[]);
bicg converged at iteration 9 to a solution with relative 
residual 5.3e-009

Alternatively, use this matrix-vector product function

function y = afun(x,n,transp_flag)
if (nargin > 2) & strcmp(transp_flag,'transp')
    y = 4 * x;
    y(1:n-1) = y(1:n-1) - 2 * x(2:n);
    y(2:n) = y(2:n) - x(1:n-1);
else
    y = 4 * x;
    y(2:n) = y(2:n) - 2 * x(1:n-1);
    y(1:n-1) = y(1:n-1) - x(2:n);
end

as input to bicg.

   x1 = bicg(@afun,b,tol,maxit,M1,M2,[],n);

Example 2. Start with A = west0479 and make the true solution the vector of all ones.

load west0479;
A = west0479;
b = sum(A,2);

You can accurately solve A*x = b using backslash since A is not so large.

x = A \ b;
norm(b-A*x) / norm(b)

ans =
    1.2454e-017

Now try to solve A*x = b with bicg.

[x,flag,relres,iter,resvec] = bicg(A,b)

flag =
          1
relres =
          1
iter =
          0

The value of flag indicates that bicg iterated the default 20 times without converging. The value of iter shows that the method behaved so badly that the initial all-zero guess was better than all the subsequent iterates. The value of relres supports this: relres = norm(b-A*x)/norm(b) = norm(b)/norm(b) = 1. You can confirm that the unpreconditioned method oscillates rather wildly by plotting the relative residuals at each iteration.

semilogy(0:20,resvec/norm(b),'-o')
xlabel('iteration number')
ylabel('relative residual')

Now, try an incomplete LU factorization with a drop tolerance of 1e-5 for the preconditioner.

[L1,U1] = luinc(A,1e-5);
Warning: Incomplete upper triangular factor has 1 zero diagonal.
         It cannot be used as a preconditioner for an iterative 
         method.

nnz(A) 
ans =
         1887
nnz(L1) 
ans =
         5562
nnz(U1) 
ans =
         4320

The zero on the main diagonal of the upper triangular U1 indicates that U1 is singular. If you try to use it as a preconditioner,

[x,flag,relres,iter,resvec] = bicg(A,b,1e-6,20,L1,U1)

flag =
         2
relres =
         1
iter =
         0
resvec =
         7.0557e+005

the method fails in the very first iteration when it tries to solve a system of equations involving the singular U1 using backslash. bicg is forced to return the initial estimate since no other iterates were produced.

Try again with a slightly less sparse preconditioner.

[L2,U2] = luinc(A,1e-6)

nnz(L2) 
ans =
         6231
nnz(U2) 
ans =
         4559

This time U2 is nonsingular and may be an appropriate preconditioner.

[x,flag,relres,iter,resvec] = bicg(A,b,1e-15,10,L2,U2)

flag =
         0
relres =
         2.0248e-16
iter =
         8

and bicg converges to within the desired tolerance at iteration number 8. Decreasing the value of the drop tolerance increases the fill-in of the incomplete factors but also increases the accuracy of the approximation to the original matrix. Thus, the preconditioned system becomes closer to inv(U)*inv(L)*L*U*x = inv(U)*inv(L)*b, where L and U are the true LU factors, and closer to being solved within a single iteration.

The next graph shows the progress of bicg using six different incomplete LU factors as preconditioners. Each line in the graph is labeled with the drop tolerance of the preconditioner used in bicg.

This does not give us any idea of the time involved in creating the incomplete factors and then computing the solution. The following graph plots the drop tolerance of the incomplete LU factors against the time to compute the preconditioner, the time to iterate once the preconditioner has been computed, and their sum, the total time to solve the problem. The time to produce the factors does not increase very quickly with the fill-in, but it does slow down the average time for an iteration. Since fewer iterations are performed, the total time to solve the problem decreases. west0479 is quite a small matrix, only 139-by-139, and preconditioned bicg still takes longer than backslash.

See Also

bicgstab, cgs, gmres, lsqr, luinc, minres, pcg, qmr, symmlq

@ (function handle), \ (backslash)

References

[1] Barrett, R., M. Berry, T. F. Chan, et al., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.

beta, betainc, betaln bicgstab