| MATLAB Function Reference |
  |
Arithmetic Operators + - * / \ ^ '
Matrix and array arithmetic
Syntax
A+B
A-B
A*B A.*B
A/B A./B
A\B A.\B
A^B A.^B
A' A.'
Description
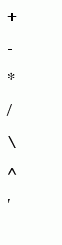 MATLAB has two different types of arithmetic operations. Matrix arithmetic operations are defined by the rules of linear algebra. Array arithmetic operations are carried out element-by-element. The period character (.) distinguishes the array operations from the matrix operations. However, since the matrix and array operations are the same for addition and subtraction, the character pairs
MATLAB has two different types of arithmetic operations. Matrix arithmetic operations are defined by the rules of linear algebra. Array arithmetic operations are carried out element-by-element. The period character (.) distinguishes the array operations from the matrix operations. However, since the matrix and array operations are the same for addition and subtraction, the character pairs .+ and .- are not used.
+
|
Addition or unary plus. A+B adds A and B. A and B must have the same size, unless one is a scalar. A scalar can be added to a matrix of any size.
|
-
|
Subtraction or unary minus. A-B subtracts B from A. A and B must have the same size, unless one is a scalar. A scalar can be subtracted from a matrix of any size.
|
*
|
Matrix multiplication. C = A*B is the linear algebraic product of the matrices A and B. More precisely,
For nonscalar A and B, the number of columns of A must equal the number of rows of B. A scalar can multiply a matrix of any size.
|
.*
|
Array multiplication. A.*B is the element-by-element product of the arrays A and B. A and B must have the same size, unless one of them is a scalar.
|
/
|
Slash or matrix right division. B/A is roughly the same as B*inv(A). More precisely, B/A = (A'\B')'. See \.
|
./
|
Array right division. A./B is the matrix with elements A(i,j)/B(i,j). A and B must have the same size, unless one of them is a scalar.
|
\
|
Backslash or matrix left division. If A is a square matrix, A\B is roughly the same as inv(A)*B, except it is computed in a different way. If A is an n-by-n matrix and B is a column vector with n components, or a matrix with several such columns, then X = A\B is the solution to the equation AX = B computed by Gaussian elimination (see "Algorithm" for details). A warning message prints if A is badly scaled or nearly singular.
|
|
If A is an m-by-n matrix with m ~= n and B is a column vector with m components, or a matrix with several such columns, then X = A\B is the solution in the least squares sense to the under- or overdetermined system of equations AX = B. The effective rank, k, of A, is determined from the QR decomposition with pivoting (see "Algorithm" for details). A solution X is computed which has at most k nonzero components per column. If k < n, this is usually not the same solution as pinv(A)*B, which is the least squares solution with the smallest norm, ||X||.
|
.\
|
Array left division. A.\B is the matrix with elements B(i,j)/A(i,j). A and B must have the same size, unless one of them is a scalar.
|
^
|
Matrix power. X^p is X to the power p, if p is a scalar. If p is an integer, the power is computed by repeated multiplication. If the integer is negative, X is inverted first. For other values of p, the calculation involves eigenvalues and eigenvectors, such that if [V,D] = eig(X), then X^p = V*D.^p/V.
|
|
If x is a scalar and P is a matrix, x^P is x raised to the matrix power P using eigenvalues and eigenvectors. X^P, where X and P are both matrices, is an error.
|
.^
|
Array power. A.^B is the matrix with elements A(i,j) to the B(i,j) power. A and B must have the same size, unless one of them is a scalar.
|
'
|
Matrix transpose. A' is the linear algebraic transpose of A. For complex matrices, this is the complex conjugate transpose.
|
.'
|
Array transpose. A.' is the array transpose of A. For complex matrices, this does not involve conjugation.
|
Remarks
The arithmetic operators have M-file function equivalents, as shown:
Binary addition
|
A+B
|
plus(A,B)
|
Unary plus
|
+A
|
uplus(A)
|
Binary subtraction
|
A-B
|
minus(A,B)
|
Unary minus
|
-A
|
uminus(A)
|
Matrix multiplication
|
A*B
|
mtimes(A,B)
|
Array-wise multiplication
|
A.*B
|
times(A,B)
|
Matrix right division
|
A/B
|
mrdivide(A,B)
|
Array-wise right division
|
A./B
|
rdivide(A,B)
|
Matrix left division
|
A\B
|
mldivide(A,B)
|
Array-wise left division
|
A.\B
|
ldivide(A,B)
|
Matrix power
|
A^B
|
mpower(A,B)
|
Array-wise power
|
A.^B
|
power(A,B)
|
Complex transpose
|
A'
|
ctranspose(A)
|
Matrix transpose
|
A.'
|
transpose(A)
|
Examples
Here are two vectors, and the results of various matrix and array operations on them, printed with format rat.
Matrix Operations
| Array Operations
|
x
|
1
2
3
|
y
|
4
5
6
|
x'
|
1 2 3
|
y'
|
4 5 6
|
x+y
|
5
7
9
|
x-y
|
-3
-3
-3
|
x + 2
|
3
4
5
|
x-2
|
-1
0
1
|
x * y
|
Error
|
x.*y
|
4
10
18
|
x'*y
|
32
|
x'.*y
|
Error
|
x*y'
|
4 5 6
8 10 12
12 15 18
|
x.*y'
|
Error
|
x*2
|
2
4
6
|
x.*2
|
2
4
6
|
x\y
|
16/7
|
x.\y
|
4
5/2
2
|
2\x
|
1/2
1
3/2
|
2./x
|
2
1
2/3
|
x/y
|
0 0 1/6
0 0 1/3
0 0 1/2
|
x./y
|
1/4
2/5
1/2
|
x/2
|
1/2
1
3/2
|
x./2
|
1/2
1
3/2
|
x^y
|
Error
|
x.^y
|
1
32
729
|
x^2
|
Error
|
x.^2
|
1
4
9
|
2^x
|
Error
|
2.^x
|
2
4
8
|
(x+i*y)'
|
1 - 4i 2 - 5i 3 - 6i
|
(x+i*y).'
|
1 + 4i 2 + 5i 3 + 6i
|
Algorithm
The specific algorithm used for solving the simultaneous linear equations denoted by X = A\B and X = B/A depends upon the structure of the coefficient matrix A.
- If
A is a triangular matrix, or a permutation of a triangular matrix, then X can be computed quickly by a permuted backsubstitution algorithm. The check for triangularity is done for full matrices by testing for zero elements and for sparse matrices by accessing the sparse data structure. Most nontriangular matrices are detected almost immediately, so this check requires a negligible amount of time.
- If
A is symmetric, or Hermitian, and has positive diagonal elements, then a Cholesky factorization is attempted (see chol). If A is found to be positive definite, the Cholesky factorization attempt is successful and requires less than half the time of a general factorization. Nonpositive definite matrices are usually detected almost immediately, so this check also requires little time. If successful, the Cholesky factorization is
A = R'*R
where R is upper triangular. The solution X is computed by solving two triangular systems,
X = R\(R'\B)
If A is sparse, a symmetric minimum degree preordering is applied (see symmmd and spparms). The algorithm is:
perm = symmmd(A); % Symmetric minimum degree reordering
R = chol(A(perm,perm)); % Cholesky factorization
y = R'\B(perm); % Lower triangular solve
X(perm,:) = R\y; % Upper triangular solve
- If
A is Hessenberg, it is reduced to an upper triangular matrix and that system is solved via substitution.
- If
A is square, but not a permutation of a triangular matrix, or is not Hermitian with positive elements, or the Cholesky factorization fails, then a general triangular factorization is computed by Gaussian elimination with partial pivoting (see lu). This results in
A = L*U
where L is a permutation of a lower triangular matrix and U is an upper triangular matrix. Then X is computed by solving two permuted triangular systems.
X = U\(L\B)
If A is sparse, a nonsymmetric minimum degree preordering is applied (see colmmd and spparms). The algorithm is
perm = colmmd(A); % Column minimum degree ordering
[L,U,P] = lu(A(:,perm)); % Cholesky factorization
Y = L\(P*B); % Lower triangular solve
X(perm,:) = U\Y; % Upper triangular solve
- If A is not square and is full, then Householder reflections are used to compute an orthogonal-triangular factorization.
A*P = Q*R
where P is a permutation, Q is orthogonal and R is upper triangular (see qr). The least squares solution X is computed with
X = P*(R\(Q'*B)
- If A is not square and is sparse, then MATLAB computes a least squares solution using the sparse
qr factorization of A.
Note
Backslash is not implemented for A not square, sparse, and complex.
|
MATLAB uses LAPACK routines to compute the various full matrix factorizations:
Matrix
|
Real
|
Complex
|
Full square, symmetric (Hermitian) positive definite
|
DLANGE, DPOTRF, DPOTRS, DPOCON
|
ZLANGE, ZPOTRF, ZPOTRS ZPOCON
|
Full square, general case
|
DLANGE, DGESV, DGECON
|
ZLANGE, ZGESV, ZGECON
|
Full non-square
|
DGEQPF, DORMQR, DTRTRS
|
ZGEQPF, ZORMQR, ZTRTRS
|
For other cases (triangular and Hessenberg) MATLAB does not use LAPACK.
|
Diagnostics
From matrix division, if a square A is singular:
Warning: Matrix is singular to working precision.
From element-wise division, if the divisor has zero elements:
Warning: Divide by zero.
The matrix division returns a matrix with each element set to Inf; the element-wise division produces NaNs or Infs where appropriate.
If the inverse was found, but is not reliable:
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = xxx
From matrix division, if a nonsquare A is rank deficient:
Warning: Rank deficient, rank = xxx tol = xxx
See Also
det, inv, lu, orth, permute, ipermute, qr, rref
References
[1] Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra,
J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen,
LAPACK User's Guide, Third Edition, SIAM, Philadelphia, 1999.
 | Reference | | Relational Operators < > <= >= == ~= |  |




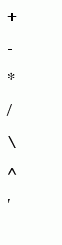 MATLAB has two different types of arithmetic operations. Matrix arithmetic operations are defined by the rules of linear algebra. Array arithmetic operations are carried out element-by-element. The period character (.) distinguishes the array operations from the matrix operations. However, since the matrix and array operations are the same for addition and subtraction, the character pairs
MATLAB has two different types of arithmetic operations. Matrix arithmetic operations are defined by the rules of linear algebra. Array arithmetic operations are carried out element-by-element. The period character (.) distinguishes the array operations from the matrix operations. However, since the matrix and array operations are the same for addition and subtraction, the character pairs 
