Mathematics

Representing BVP Problems

This section describes:

• The process for solving boundary value problems (BVPs) using the MATLAB solver, bvp4c
• Finding unknown parameters
• Evaluating the solution at specific points

Example: Mathieu's Equation

This example determines the fourth eigenvalue of Mathieu's Equation. It illustrates how to write second-order differential equations as a system of two first-order ODEs and how to use bvp4c to determine an unknown parameter .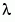

The task is to compute the fourth (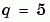) eigenvalue 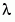of Mathieu's equation

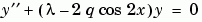
Because the unknown parameter 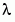is present, this second-order differential equation is subject to three boundary conditions

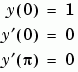
Note    The demo mat4bvp contains the complete code for this example. The demo uses subfunctions to place all functions required by bvp4c in a single M-file. To run this example type mat4bvp at the command line. See BVP Solver Basic Syntax for more information.

1 Rewrite the Problem as a First-Order System.   To use bvp4c, you must rewrite the equations as an equivalent system of first-order differential equations. Using a substitution 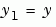and 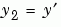, the differential equation is written as a system of two first-order equations

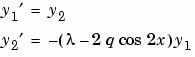
Note that the differential equations depend on the unknown parameter 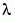. The boundary conditions become

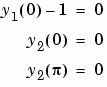
2 Code the System of First-Order ODEs in MATLAB.   Once you represent the equation as a first-order system, you can code it as a function that bvp4c can use. Because there is an unknown parameter, the function must be of the form

dydx = odefun(x,y,parameters)

The code below represents the system in the MATLAB function, mat4ode.

function dydx = mat4ode(x,y,lambda)
q = 5;
dydx = [   y(2)
         -(lambda - 2*q*cos(2*x))*y(1) ];

See Finding Unknown Parameters for more information about using unknown parameters with bvp4c.

3 Code the Boundary Conditions Function.   You must also code the boundary conditions in a MATLAB function. Because there is an unknown parameter, the function must be of the form

res = bcfun(ya,yb,parameters)

The code below represents the boundary conditions in the MATLAB function, mat4bc.

function res = mat4bc(ya,yb,lambda)
res = [  ya(2) 
         yb(2) 
        ya(1)-1 ];

4 Create an Initial Guess.   To form the guess structure solinit with bvpinit, you need to provide initial guesses for both the solution and the unknown parameter.

The function mat4init provides an initial guess for the solution. mat4init uses 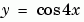because this function satisfies the boundary conditions and has the correct qualitative behavior (the correct number of sign changes).

function yinit = mat4init(x)
yinit = [  cos(4*x)
          -4*sin(4*x) ];

In the call to bvpinit, the third argument, lambda, provides an initial guess for the unknown parameter .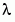

lambda = 15;
solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda);

This example uses @ to pass mat4init as a function handle to bvpinit.

Note    See the function_handle (@), func2str, and str2func reference pages, and the Function Handles chapter of "Programming and Data Types" in the MATLAB documentation for information about function handles.

5 Apply the BVP Solver.   The mat4bvp example calls bvp4c with the functions mat4ode and mat4bc and the structure solinit created with bvpinit.

sol = bvp4c(@mat4ode,@mat4bc,solinit);

6 View the Results.   Complete the example by displaying the results:

• Print the value of the unknown parameter found by bvp4c.

fprintf('The fourth eigenvalue is approximately %7.3f.\n',...
        sol.parameters)

• Use bvpval to evaluate the numerical solution at 100 equally spaced points in the interval 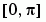, and plot its first component. This component approximates .

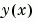xint = linspace(0,pi);
Sxint = bvpval(sol,xint);
plot(xint,Sxint(1,:))
axis([0 pi -1 1.1])
title('Eigenfunction of Mathieu''s equation.') 
xlabel('x')
ylabel('solution y')

See Evaluating the Solution at Specific Points for information about using bvpval.

The following plot shows the eigenfunction associated with the final eigenvalue 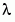= 17.097.

Finding Unknown Parameters

The bvp4c solver can find unknown parameters 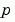for problems of the form

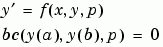
You must provide bvp4c an initial guess for any unknown parameters in the vector solinit.parameters. When you call bvpinit to create the structure solinit, specify the initial guess as a vector in the additional argument parameters.

solinit = bvpinit(x,v,parameters)

The bvp4c function arguments odefun and bcfun must each have a third argument.

dydx = odefun(x,y,parameters)
res = bcfun(ya,yb,parameters)

The bvp4c solver calculates intermediate values of unknown parameters at each iteration, and passes the latest values to odefun and bcfun in the parameters arguments. The solver returns the final values of these unknown parameters in sol.parameters.

Evaluating the Solution at Specific Points

The collocation method implemented in bvp4c produces a C¹-continuous solution over the whole interval of integration 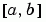. You can evaluate the approximate solution, 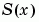, at any point in 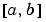using the structure sol returned by bvp4c and the helper function bvpval

Sxint = bvpval(sol,xint)

The bvpval function is vectorized. For a vector xint, the ith column of Sxint approximates the solution .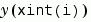

Boundary Value Problem Solver

Making a Good Initial Guess