

| Mathematics |   |
Making a Good Initial Guess
To solve a boundary value problem, you need to provide an initial guess for the solution. The quality of your initial guess can be critical to the solver performance, and to being able to solve the problem at all. However, coming up with a sufficiently good guess can be the most challenging part of solving a boundary value problem. Certainly, you should apply the knowledge of the problem's physical origin.
One way of arriving at a good guess is to solve the problem as a sequence of relatively simpler problems, i.e., a continuation. The solution of one problem might yield a good initial guess for solving the next problem.
The following example illustrates how you can solve a difficult problem using continuation.
Note
The demo shockbvp contains the complete code for this example. The demo uses subfunctions to place all required functions in a single M-file. To run this example type shockbvp at the command line. See BVP Solver Basic Syntax and Representing BVP Problems for more information.
|
Example: Using Continuation to Solve a Difficult BVP
This example solves the differential equation
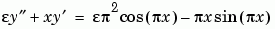
for 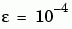 , on the interval [-1 1], with boundary conditions
, on the interval [-1 1], with boundary conditions 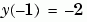 and
and 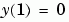 . For
. For 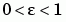 , the solution has a transition layer at
, the solution has a transition layer at 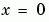 . Because of this rapid change in the solution for small values of
. Because of this rapid change in the solution for small values of 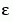 , the problem becomes difficult to solve numerically.
, the problem becomes difficult to solve numerically.
| Note This problem appears in [1] to illustrate the mesh selection capability of a well established BVP code COLSYS. |
1 Code the ODE and Boundary Condition Functions. Code the differential equation and the boundary conditions as functions that bvp4c can use. Because there is an additional known parameter 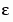 , the functions must be of the form
, the functions must be of the form
dydx = odefun(x,y,p1) res = bcfun(ya,yb,p1)
The code below represents the differential equation and the boundary conditions in the MATLAB functions shockODE and shockBC. The additional parameter 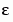 is represented by
is represented by e.
function dydx = shockODE(x,y,e)
pix = pi*x;
dydx = [ y(2)
-x/e*y(2) - pi^2*cos(pix) - pix/e*sin(pix) ];
function res = shockBC(ya,yb,e)
res = [ ya(1)+2
yb(1) ];
The example passes e as an additional input argument to bvp4c.
sol = bvp4c(@shockODE,@shockBC,sol,options,e);
bvp4c then passes this argument to the functions shockODE and shockBC when it evaluates them. See Additional BVP Solver Arguments for more information.
2 Provide Analytical Partial Derivatives. For this problem, the solver benefits from using analytical partial derivatives. The code below represents the derivatives in functions shockJac and shockBCJac.
function jac = shockJac(x,y,e)
jac = [ 0 1
0 -x/e ];
function [dBCdya,dBCdyb] = shockBCJac(ya,yb,e)
dBCdya = [ 1 0
0 0 ];
dBCdyb = [ 0 0
1 0 ];
shockJac and shockBCJac must accept the additional argument e, because bvp4c passes the additional argument to all the functions the user supplies.
Tell bvp4c to use these functions to evaluate the partial derivatives by setting the options FJacobian and BCJacobian.
options = bvpset('FJacobian',@shockJac,...
'BCJacobian',@shockBCJac);
3 Create an Initial Guess. You must provide bvp4c with a guess structure that contains an initial mesh and a guess for values of the solution at the mesh points. A constant guess of 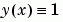 and
and 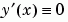 , and a mesh of five equally spaced points on [-1 1] suffice to solve the problem for
, and a mesh of five equally spaced points on [-1 1] suffice to solve the problem for 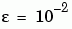 . Use
. Use bvpinit to form the guess structure.
sol = bvpinit([-1 -0.5 0 0.5 1],[1 0]);
4 Use Continuation to Solve the Problem. To obtain the solution for the parameter 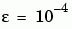 , the example uses continuation by solving a sequence of problems for
, the example uses continuation by solving a sequence of problems for 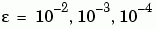 . The solver
. The solver bvp4c does not perform continuation automatically, but the code's user interface has been designed to make continuation easy. The code uses the output sol that bvp4c produces for one value of e as the guess in the next iteration.
e = 0.1;
for i=2:4
e = e/10;
sol = bvp4c(@shockODE,@shockBC,sol,options,e);
end
5 View the Results. Complete the example by displaying the final solution
plot(sol.x,sol.y(1,:))
axis([-1 1 -2.2 2.2])
title(['There is a shock at x = 0 when \epsilon ='...
sprintf('%.e',e) '.'])
xlabel('x')
ylabel('solution y')
 | Representing BVP Problems | Improving BVP Solver Performance |  |