

| Symbolic Math Toolbox |   |
Extended Calculus Example
The function
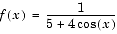
syms x f = 1/(5+4*cos(x))store the symbolic expression defining the function in
f.
The function ezplot(f) produces the plot of f(x) as shown below.
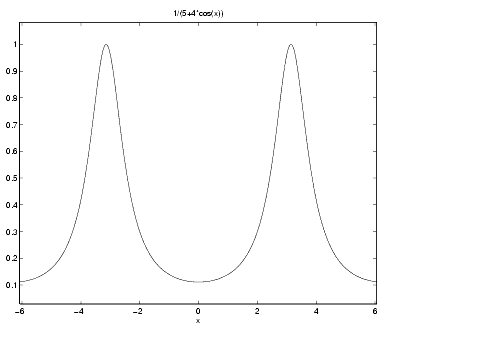
The ezplot function tries to make reasonable choices for the range of the x-axis and for the resulting scale of the y-axis. Its choices can be overridden by an additional input argument, or by subsequent axis commands. The default domain for a function displayed by ezplot is 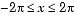 . To produce a graph of f (x) for
. To produce a graph of f (x) for 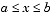 , type
, type
ezplot(f,[a b])Let's now look at the second derivative of the function
f.
f2 = diff(f,2) f2 = 32/(5+4*cos(x))^3*sin(x)^2+4/(5+4*cos(x))^2*cos(x)Equivalently, we can type
f2 = diff(f,x,2). The default scaling in ezplot cuts off part of f2's graph. Set the axes limits manually to see the entire function.
ezplot(f2) axis([-2*pi 2*pi -5 2])
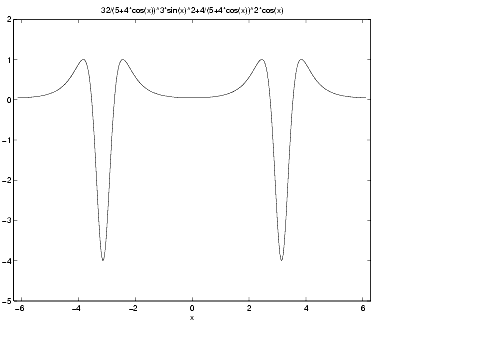 From the graph, it appears that the values of f ´´ (x) lie between -4 and 1. As it turns out, this is not true. We can calculate the exact range for
From the graph, it appears that the values of f ´´ (x) lie between -4 and 1. As it turns out, this is not true. We can calculate the exact range for f (i.e., compute its actual maximum and minimum).
The actual maxima and minima of f ´´ (x) occur at the zeros of f ´´´ (x). The statements
f3 = diff(f2); pretty(f3)compute f ´´´ (x) and display it in a more readable format.
3 sin(x) sin(x) cos(x) sin(x) 384 --------------- + 96 --------------- - 4 --------------- 4 3 2 (5 + 4 cos(x)) (5 + 4 cos(x)) (5 + 4 cos(x))We can simplify and this expression using the statements
f3 = simple(f3);
pretty(f3)
2 2
sin(x) (96 sin(x) + 80 cos(x) + 80 cos(x) - 25)
4 -------------------------------------------------
4
(5 + 4 cos(x))
Now use the solve function to find the zeros of f ´´´ (x).
z = solve(f3)
each of whose entries is a zero of f ´´´ (x). The commandsz =[ 0][ atan((-255-60*19^(1/2))^(1/2),10+3*19^(1/2))][ atan(-(-255-60*19^(1/2))^(1/2),10+3*19^(1/2))][ atan((-255+60*19^(1/2))^(1/2)/(10-3*19^(1/2)))+pi][ -atan((-255+60*19^(1/2))^(1/2)/(10-3*19^(1/2)))-pi]
format; % Default format of 5 digits zr = double(z)convert the zeros to
double form.
zr =
0
0+ 2.4381i
0- 2.4381i
2.4483
-2.4483
So far, we have found three real zeros and two complex zeros. However, a graph of f3 shows that we have not yet found all its zeros.
ezplot(f3)
hold on;
plot(zr,0*zr,'ro')
plot([-2*pi,2*pi], [0,0],'g-.');
title('Zeros of f3')
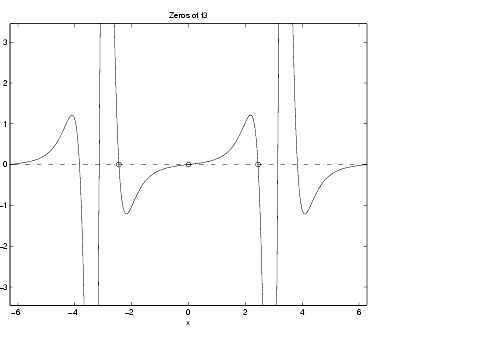
This occurs because f ´´´ (x) contains a factor of sin(x), which is zero at integer multiples of 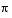 . The function,
. The function, solve(sin(x)), however, only reports the zero at x = 0.
We can obtain a complete list of the real zeros by translating zr
zr = [0 zr(4) pi 2*pi-zr(4)]by multiples of
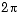
zr = [zr-2*pi zr zr+2*pi];Now let's plot the transformed
zr on our graph for a complete picture of the zeros of f3.
plot(zr,0*zr,'kX')The first zero of f ´´´ (x) found by
solve is at x = 0. We substitute 0 for the symbolic variable in f2
f20 = subs(f2,x,0)to compute the corresponding value of f ´´ (0).
f20 =
0.0494
A look at the graph of f ´´ (x) shows that this is only a local minimum, which we demonstrate by replotting f2.
clf
ezplot(f2)
axis([-2*pi 2*pi -4.25 1.25])
ylabel('f2');
title('Plot of f2 = f''''(x)')
hold on
plot(0,double(f20),'ro')
text(-1,-0.25,'Local minimum')
The resulting plot
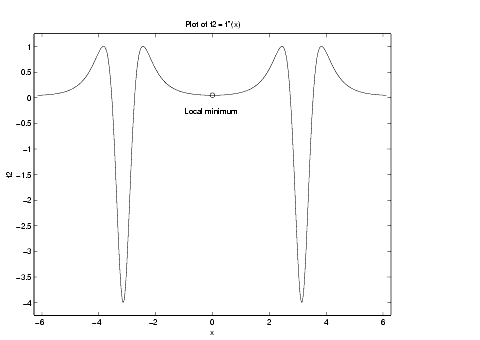
indicates that the global minima occur near 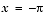 and
and 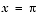 . We can demonstrate that they occur exactly at
. We can demonstrate that they occur exactly at 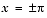 , using the following sequence of commands. First we try substituting
, using the following sequence of commands. First we try substituting 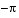 and
and 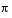 into f ´´´ (x).
into f ´´´ (x).
simple([subs(f3,x,-sym(pi)),subs(f3,x,sym(pi))])The result
ans = [ 0, 0]shows that
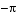 and
and 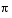 happen to be critical points of f ´´´ (x). We can see that
happen to be critical points of f ´´´ (x). We can see that 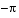 and
and 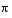 are global minima by plotting
are global minima by plotting f2(-pi) and f2(pi) against f2(x).
m1 = double(subs(f2,x,-pi)); m2 = double(subs(f2,x,pi)); plot(-pi,m1,'go',pi,m2,'go') text(-1,-4,'Global minima')The actual minima are
m1, m2
ans = [ -4, -4]as shown in the following plot.
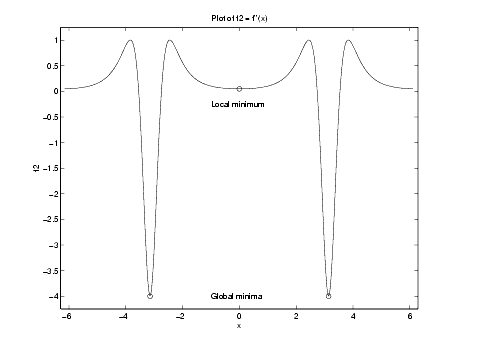
The foregoing analysis confirms part of our original guess that the range of
f´´ (x) is [-4, 1]. We can confirm the other part by examining the fourth zero of f´´´ (x) found by solve. First extract the fourth zero from z and assign it to a separate variable
s = z(4)to obtain
s = atan((-255+60*19^(1/2))^(1/2)/(10-3*19^(1/2)))+piExecuting
sd = double(s)displays
the zero's corresponding numeric value.
sd = 2.4483Plotting the point
(s, f2(s)) against f2, using
M1 = double(subs(f2,x,s)); plot(sd,M1,'ko') text(-1,1,'Global maximum')visually confirms that
s is a maximum.
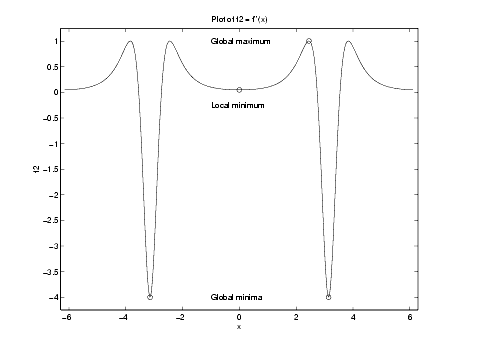 Therefore, our guess that the maximum of f ´´ (x) is [-4, 1] was close, but incorrect. The actual range is [-4, 1.0051].
Now, let's see if integrating f ´´ (x) twice with respect to x recovers our original function f(x) = 1/(5 + 4 cos x). The command
Therefore, our guess that the maximum of f ´´ (x) is [-4, 1] was close, but incorrect. The actual range is [-4, 1.0051].
Now, let's see if integrating f ´´ (x) twice with respect to x recovers our original function f(x) = 1/(5 + 4 cos x). The command
g = int(int(f2))
This is certainly not the original expression for f(x). Let's look at the difference f(x)-g(x).g =-8/(tan(1/2*x)^2+9)
d = f - g
pretty(d)
1 8
------------ + ---------------
5 + 4 cos(x) 2
tan(1/2 x) + 9
We can simplify this using simple(d) or simplify(d). Either command produces
ans = 1This illustrates the concept that differentiating f(x) twice, then integrating the result twice, produces a function that may differ from f(x) by a linear function of x. Finally, integrate f(x) once more.
F = int(f)The result
F = 2/3*atan(1/3*tan(1/2*x))involves the arctangent function. Though F(x) is the antiderivative of a continuous function, it is itself discontinuous as the following plot shows.
ezplot(F)Note that F(x) has jumps at
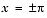 . This occurs because tan x is singular at
. This occurs because tan x is singular at 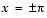 .
In fact, as
.
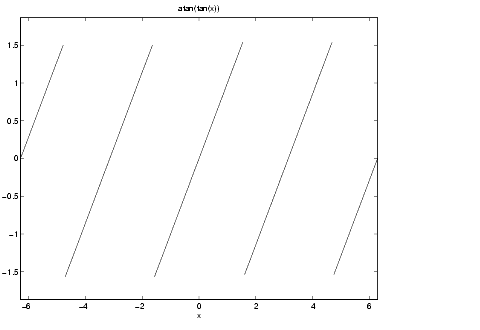
In fact, as
ezplot(atan(tan(x)))shows, the numerical value of
atan(tan(x))differs from x by a piecewise constant function that has jumps at odd multiples of 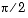 .
.
To obtain a representation of F(x) that does not have jumps at these points, we must introduce a second function, J(x), that compensates for the discontinuities. Then we add the appropriate multiple of J(x) to F(x).
J = sym('round(x/(2*pi))');
c = sym('2/3*pi');
F1 = F+c*J
F1 =
2/3*atan(1/3*tan(1/2*x))+2/3*pi*round(1/2*x/pi)
and plot the result.
ezplot(F1,[-6.28,6.28])This representation does have a continuous graph.
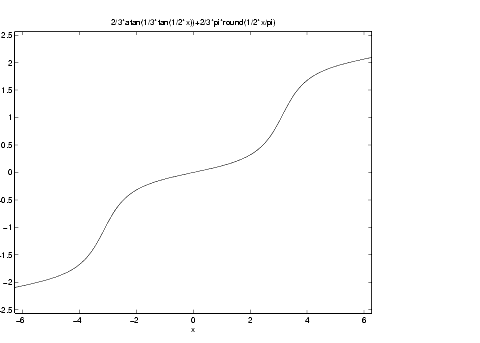
Notice that we use the domain [-6.28, 6.28] in ezplot rather than the default domain 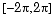 . The reason for this is to prevent an evaluation of F1 = 2/3 atan(1/3 tan 1/2 x) at the singular points
. The reason for this is to prevent an evaluation of F1 = 2/3 atan(1/3 tan 1/2 x) at the singular points 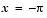 and
and 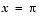 where the jumps in F and J do not cancel out one another. The proper handling of branch cut discontinuities in multivalued functions like arctan x is a deep and difficult problem in symbolic computation. Although MATLAB and Maple cannot do this entirely automatically, they do provide the tools for investigating such questions.
where the jumps in F and J do not cancel out one another. The proper handling of branch cut discontinuities in multivalued functions like arctan x is a deep and difficult problem in symbolic computation. Although MATLAB and Maple cannot do this entirely automatically, they do provide the tools for investigating such questions.
 | Taylor Series | Simplifications and Substitutions |  |