| Symbolic Math Toolbox |
  |
Taylor Series
The statements
syms x
f = 1/(5+4*cos(x))
T = taylor(f,8)
return
T =
1/9+2/81*x^2+5/1458*x^4+49/131220*x^6
which is all the terms up to, but not including, order eight (O(x8)) in the Taylor series for f(x).
Technically, T is a Maclaurin series, since its basepoint is a = 0.
The command
pretty(T)
prints T in a format resembling typeset mathematics.
2 4 49 6
1/9 + 2/81 x + 5/1458 x + ------ x
131220
These commands
syms x
g = exp(x*sin(x))
t = taylor(g,12,2)
generate the first 12 nonzero terms of the Taylor series for g about x = 2.
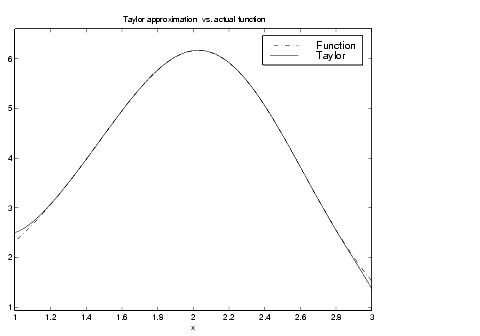
Let's plot these functions together to see how well this Taylor approximation compares to the actual function g.
xd = 1:0.05:3; yd = subs(g,x,xd);
ezplot(t, [1,3]); hold on;
plot(xd, yd, 'r-.')
title('Taylor approximation vs. actual function');
legend('Function','Taylor')
Special thanks to Professor Gunnar Bäckstrøm of UMEA in Sweden for this example.
 | Symbolic Summation | | Extended Calculus Example |  |