Statistics Toolbox

Noncentral t Distribution

The following sections provide an overview of the noncentral t distribution.

Background of the Noncentral t Distribution.   The noncentral t distribution is a generalization of the familiar Student's t distribution.

If x and s are the mean and standard deviation of an independent random sample of size n from a normal distribution with mean µ and 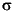² = n, then

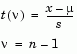
Suppose that the mean of the normal distribution is not µ. Then the ratio has the noncentral t distribution. The noncentrality parameter is the difference between the sample mean and µ.

The noncentral t distribution allows us to determine the probability that we would detect a difference between x and µ in a t test. This probability is the power of the test. As x-µ increases, the power of a test also increases.

Definition of the Noncentral t Distribution.   The most general representation of the noncentral t distribution is quite complicated. Johnson and Kotz (1970) give a formula for the probability that a noncentral t variate falls in the range [-t, t].

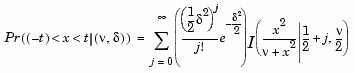
I(x|a,b) is the incomplete beta function with parameters a and b, 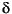 is the noncentrality parameter, and  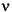is the degrees of freedom.

Example and Plot of the Noncentral t Distribution.   The following commands generate a plot of the noncentral t pdf.

x = (-5:0.1:5)';
p1 = nctcdf(x,10,1);
p = tcdf(x,10);
plot(x,p,'--',x,p1,'-')

Student's t Distribution

Uniform (Continuous) Distribution