Statistics Toolbox

pdist

Pairwise distance between observations.

Syntax

Y = pdist(X)
Y = pdist(X,'metric')
Y = pdist(X,'minkowski',p)

Description

Y = pdist(X) computes the Euclidean distance between pairs of objects in m-by-n matrix X, which is treated as m vectors of size n. For a dataset made up of m objects, there are 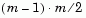pairs.

The output, Y, is a vector of length 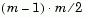, containing the distance information. The distances are arranged in the order (1,2), (1,3), ..., (1,m), (2,3), ..., (2,m), ..., ..., (m-1,m). Y is also commonly known as a similarity matrix or dissimilarity matrix.

To save space and computation time, Y is formatted as a vector. However, you can convert this vector into a square matrix using the squareform function so that element i,j in the matrix corresponds to the distance between objects i and j in the original dataset.

Y = pdist(X,'metric') computes the distance between objects in the data matrix, X, using the method specified by 'metric', where 'metric' can be any of the following character strings that identify ways to compute the distance.

String	Meaning
'Euclid'	Euclidean distance (default)
'SEuclid'	Standardized Euclidean distance
'Mahal'	Mahalanobis distance
'CityBlock'	City Block metric
'Minkowski'	Minkowski metric

Y = pdist(X,'minkowski',p) computes the distance between objects in the data matrix, X, using the Minkowski metric. p is the exponent used in the Minkowski computation which, by default, is 2.

Mathematical Definitions of Methods

Given an m-by-n data matrix X, which is treated as m (1-by-n) row vectors x₁, x₂, ..., x_m, the various distances between the vector x_r and x_s are defined as follows:

• Euclidean distance

• Standardized Euclidean distance

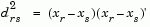
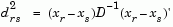
where D is the diagonal matrix with diagonal elements given by

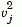, which denotes the variance of the variable X_j over the m objects.

• Mahalanobis distance

where V is the sample covariance matrix.

• City Block metric

• Minkowski metric

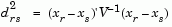
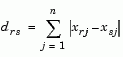
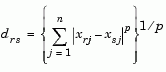
Notice that for the special case of p = 1, the Minkowski metric gives the City Block metric, and for the special case of p = 2, the Minkowski metric gives the Euclidean distance.

Examples

X = [1 2; 1 3; 2 2; 3 1]
X =
     1     2
     1     3
     2     2
     3     1
Y = pdist(X,'mahal')
Y =
    2.3452    2.0000    2.3452    1.2247    2.4495    1.2247
Y = pdist(X)
Y =
    1.0000    1.0000    2.2361    1.4142    2.8284    1.4142
squareform(Y)
ans =
         0    1.0000    1.0000    2.2361
    1.0000         0    1.4142    2.8284
    1.0000    1.4142         0    1.4142
    2.2361    2.8284    1.4142         0

See Also

cluster, clusterdata, cophenet, dendrogram, inconsistent, linkage, squareform

pdf

perms