Spline Toolbox

Splines: An Overview

Polynomials are the approximating functions of choice when a smooth function is to be approximated locally. For example, the truncated Taylor series

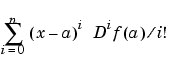
provides a satisfactory approximation for f(x) if f is sufficiently smooth and x is sufficiently close to a. But if a function is to be approximated on a larger interval, the degree, n, of the approximating polynomial may have to be chosen unacceptably large. The alternative is to subdivide the interval [a..b] of approximation into sufficiently small intervals 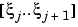, with

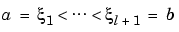, so that, on each such interval, a polynomial p_j of relatively low degree can provide a good approximation to f. This can even be done in such a way that the polynomial pieces blend smoothly, i.e., so that the resulting patched or composite function s(x) := p_j(x) for 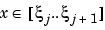, all j, has several continuous derivatives. Any such smooth piecewise polynomial function is called a spline. I.J. Schoenberg coined this term since a twice continuously differentiable cubic spline with sufficiently small first derivative approximates the shape of a draftsman's spline.

There are two commonly used ways to represent a spline, the ppform and the B-form. In this toolbox, a spline in ppform is often referred to as a piecewise polynomial, while a piecewise polynomial in B-form is often referred to as a spline. This reflects the fact that piecewise polynomials and splines are just two different views of the same thing.

The ppform of a spline of order k provides a description in terms of its breaks 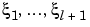and the local polynomial coefficients c_ji of its l pieces.

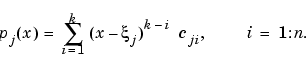
For example, a cubic spline is of order 4, corresponding to the fact that it requires four coefficients to specify a cubic polynomial. The ppform is convenient for the evaluation and other uses of a spline.

The B-form has become the standard way to represent a spline during its construction, since the B-form makes it easy to build in smoothness requirements across breaks and leads to banded linear systems. The B-form describes a spline as a weighted sum

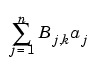
of B-splines of the required order k, with their number, n, at least as big as k-1 plus the number of polynomial pieces that make up the spline. Here, B_j,k := 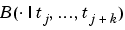is the jth B-spline of order k for the knot sequence 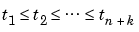. In particular, B_j,k is piecewise-polynomial of degree < k, with breaks t_j, ..., t_j+k, is nonnegative, is zero outside the interval ( t_j .. t_j+k), and is so normalized that  

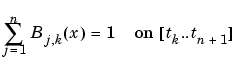
The multiplicity of the knots governs the smoothness, in the following way: If the number 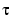occurs exactly r times in the sequence t_j, ..., t_j+k, then B_j,k and its first k - r - 1 derivatives are continuous across the break 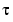, while the (k - r)th derivative has a jump at 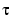. All these properties of the B-spline are nicely visualized and experimented with interactively with the command bspligui.

Since B_j,k is nonzero only on the interval ( t_j .. t_j+k), the linear system for the B-spline coefficients of the spline to be determined, by interpolation or least-squares approximation, or even as the approximate solution of some differential equation, is banded, making the solving of that linear system particularly easy. For example, if a spline s of order k with knot sequence 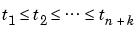is to be constructed so that s(x_i) = y_i for i=1,...,n, then we are led to the linear system

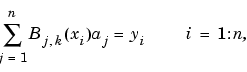
for the unknown B-spline coefficients a_j in which each equation has at most k nonzero entries.

Also, many theoretical facts concerning splines are most easily stated and/or proved in terms of B-splines. For example, it is possible to match arbitrary data at sites 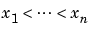uniquely by a spline of order k with knot sequence t₁, ..., t_n+k if and only if 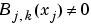for all j (Schoenberg-Whitney Conditions). Computations with B-splines are facilitated by stable recurrence relations

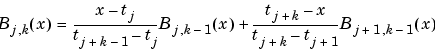
that are also of help in the conversion from B-form to ppform. The dual functional   

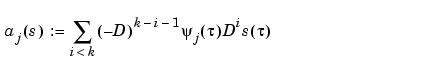
provides a useful expression for the jth B-spline coefficient of the spline s in terms of its value and derivatives at an arbitrary site 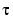between t_j and t_j+k, and with

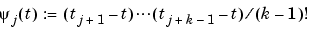. It can be used to show that a_j(s) is closely related to s on the interval [t_j..t_j+k], and seems the most efficient means for converting from ppform to B-form.

The above constructive approach is not the only avenue to splines. In the variational approach, a spline is obtained as a best interpolant, e.g., as the function with smallest mth derivative among all those matching prescribed function values at certain sites. As it turns out, among the many such splines available, only those that are piecewise-polynomials or, perhaps, piecewise- exponentials have found much use. Of particular practical interest is the smoothing spline 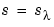which, for given data (x_i,y_i) with 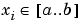, all i, and given corresponding positive weights w_i, and for given smoothing parameter 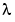, minimizes

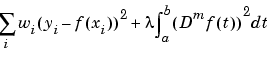
over all functions f with m derivatives. It turns out that the smoothing spline s is a spline of order 2m with a break at every data site. The art of using the smoothing spline consists in choosing 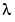so that s contains as much of the information, and as little of the supposed noise, in the data as possible.

Multivariate splines can be obtained from univariate splines by the tensor product construct. For example, a trivariate spline in B-form is given by

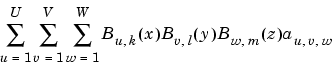
This spline is of order k in x, of order l in y, and of order m in z. Similarly, the ppform of a tensor-product spline is specified by break sequences in each of the variables and, for each (hyper-)rectangle thereby specified, a coefficient array. Further, as in the univariate case, the coefficients may be vectors, typically 2-vectors or 3-vectors, making it possible to represent, e.g., certain surfaces in 3-space.

Tutorial

The ppform