Spline Toolbox

Tutorial

Some Simple Examples

Here are some simple ways to make use of the commands in this toolbox. More complicated examples are given in later sections. Other examples are available in the various demos, all of which can be reached by MATLAB's demos command. In addition, the command splinetool provides a GUI for you to try several of the basic spline interpolation and approximation commands from this toolbox on your data; it even provides various instructive data sets.

Check the reference pages if you have specific questions about the use of the commands mentioned. Check the Glossary if you have specific questions about the terminology used; a look into the index may help.

Suppose you want to interpolate to some smooth data, for example to

x = (4*pi)*[0 1 rand(1,20)]; y = sin(x);

Then you could try the cubic spline interpolant obtained by

cs = csapi(x,y);

and plotted, along with the data, by

fnplt(cs); hold on, plot(x,y,'o')
legend('cubic spline','data'), hold off

This produces a figure like the following:

Figure 1-1: Cubic Spline Interpolant to Some Smooth Data

This is, more precisely, the cubic spline interpolant with the not-a-knot end conditions, meaning that it is the unique piecewise cubic polynomial with two continuous derivatives with breaks at all interior data sites except for the leftmost and the rightmost one. It is the same interpolant as produced by MATLAB's command spline(x,y).

We know that the sine function is 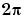-periodic. To check how well our interpolant does on that score, we compute, e.g., the difference in the value of its first derivative at the two endpoints,

» diff(fnval(fnder(cs),[0 4*pi]))
ans = -.0307

which is not so good. If you prefer to get an interpolant whose first and second derivatives at the two endpoints, 0 and 4*pi, match, use instead the command cspape which permits specification of many different kinds of end conditions, including periodic end conditions. So, use instead

pcs = csape(x,y,'periodic');

for which we get

» diff(fnval(fnder(pcs),[0 4*pi]))
ans = -2.2204e-016

as the difference of end slopes. Even the difference in end second derivatives is small:

» diff(fnval(fnder(pcs,2),[0 4*pi]))
ans = -1.4017e-014

Other end conditions can be handled as well. For example,

cs = csape(x,y,[1 2],[3 -4]);

provides the cubic spline interpolant with breaks at the x(i) and with its slope at the leftmost data site equal to 3, and its second derivative at the rightmost data site equal to -4.

If you want to interpolate at sites other than the breaks and/or by splines other than cubic splines with simple knots, then you use the spapi command. In its simplest form, you would say

sp = spapi(k,x,y);

in which the first argument, k, specifies the order of the interpolating spline; this is the number of coefficients in each polynomial piece, i.e., 1 more than the nominal degree of its polynomial pieces. For example, the next figure shows a linear, a quadratic, and a quartic spline interpolant to our data, as obtained by the statements

sp2 = spapi(2,x,y); fnplt(sp2), hold on
sp3 = spapi(3,x,y); fnplt(sp3,'--')
sp5 = spapi(5,x,y); fnplt(sp5,'-.'), plot(x,y,'o')
legend('linear','quadratic','quartic','data'), hold off

Figure 1-2: Spline Interpolants of Various Orders to Smooth Data

Even the cubic spline interpolant obtained from spapi is different from the one provided by csapi and spline. To emphasize their difference, we compute and plot their second derivatives, as follows:

fnplt(fnder(spapi(4,x,y),2)), hold on
fnplt(fnder(csapi(x,y),2),1.5),plot(x,zeros(size(x)),'o')
legend('from spapi','from csapi','data sites'), hold off

This gives the following graph:

Figure 1-3: Second Derivative of Two Cubic Spline Interpolants to the Same Smooth Data

Since the second derivative of a cubic spline is a broken line, with vertices at the breaks of the spline, we can see clearly that csapi places breaks at the data sites, while spapi does not, and thereby produces a less jerky second derivative in this example.

It is, in fact, possible to specify explicitly just where the spline interpolant should have its breaks, using the command

sp = spapi(knots,x,y);

in which the sequence knots supplies, in a certain way, the breaks to be used. For example, recalling that we had chosen y to be sin(x), the command

ch = spapi(augknt(x,4,2),[x x],[y cos(x)]);

provides a cubic Hermite interpolant to the sine function, namely the piecewise cubic function, with breaks at all the x(i)'s, that matches the sine function in value and slope at all the x(i)'s. This makes the interpolant continuous with continuous first derivative but, in general, it has jumps across the breaks in its second derivative. Just how does this command know which part of the data value array [y cos(x)] supplies the values and which the slopes? Notice that the data site array here is given as [x x], i.e., each data site appears twice. One of the first things done in spapi is to check whether the data site array is nondecreasing and to reorder it to make it so if need be, in which case the data value array is reordered in the same way. In this way, y(i) is associated with the first occurrence of x(i), and cos(x(i)) is associated with the second occurrence of x(i). The data value associated with the first appearance of a data site is taken to be a function value; the data value associated with the second appearance is taken to be a slope. If there were a third appearance of that data site, the corresponding data value would be taken as the second derivative value to be matched at that site. See the section entitled ``The B-form'' for a discussion of the command augknt used here to generate the appropriate "knot sequence".

What if the data are noisy? For example, suppose that the given values are

noisy = y + .1*(rand(size(x))-.5);

Then you might prefer to approximate instead. For example, you might try the cubic smoothing spline, obtained by the command

scs = csaps(x,noisy);

and plotted by

fnplt(scs), hold on, plot(x,noisy,'o')
legend('smoothing spline','noisy data'), hold off

This produces a figure like this:

Figure 1-4: Cubic Smoothing Spline to Noisy Data

If you don't like the level of smoothing done by csaps(x,y), you can change it by specifying the smoothing parameter, p, as an optional third argument. Choose this number anywhere between 0 and 1. As p changes from 0 to 1, the smoothing spline changes, correspondingly, from one extreme, the least-squares straight-line approximation to the data, to the other extreme, the "natural" cubic spline interpolant to the data. Since csaps returns the smoothing parameter actually used as an optional second output, you could now experiment, as follows:

[scs,p] = csaps(x,noisy); fnplt(scs), hold on
fnplt(csaps(x,noisy,p/2),'--')
fnplt(csaps(x,noisy,(1+p)/2),':'), plot(x,noisy,'o')
legend('smoothing spline','more smoothed','less smoothed',...
'noisy data'), hold off

This produces the following picture.

Figure 1-5: Noisy Data More or Less Smoothed

At times, you might prefer simply to get the smoothest cubic spline sp that is within a specified tolerance tol of the given data in the sense that

norm(noisy - fnval(sp,x))^2 <= tol

This spline is provided by the command

sp = spaps(x,noisy,tol);

If a least-squares approximant is wanted instead, it is provided by the statement

sp = spap2(knots,k,x,y);

in which both the knot sequence knots and the order k of the spline must be provided.

The popular choice for the order is 4, and that gives you a cubic spline. If you have no clear idea of how to choose the knots, simply specify the number of polynomial pieces you want used. For example,

sp = spap2(3,4,x,y); 

gives a cubic spline consisting of three polynomial pieces. If the resulting error is uneven, you might try for a better knot distribution by using newknt as follows:

sp = spap2(newknt(sp),4,x,y);

If f is one of these splines cs, ch, or sp so constructed, then, as we saw already, it can be displayed by the statement

fnplt(f) 

Its value at a is given by the statement

fnval(f,a);

Its second derivative is constructed by the statement

DDf = fnder(fnder(f));

or by the statement

DDf = fnder(f,2);

Its definite integral over the interval [a..b] is supplied by the statement

[1 -1]*fnval(fnint(f),[b;a]);

and the difference between the spline in cs and the one in ch can be computed as

fncmb(cs,'-',sp);

The toolbox supports vector-valued splines. For example, if you want a spline curve through given planar points (x(i), y(i)), i = 1, ..., n, then the statements

xy = [x;y]; df = diff(xy.').'; 
t = cumsum([0, sqrt([1 1]*(df.*df))]); 
cv = csapi(t,xy);

provide such a spline curve, using chord-length parametrization and cubic spline interpolation with the not-a-knot end condition, as can be verified by the statements

fnplt(cv), hold on, plot(x,y,'o'), hold off

As another example of the use of vector-valued functions, suppose that you have solved the equations of motion of a particle in some specified force field in the plane, obtaining, at discrete times 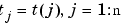, the position 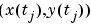as well as the velocity 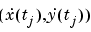stored in the 4-vector 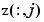, as you would if, in the standard way, you had solved the equivalent first-order system numerically. Then the following statement, which uses cubic Hermite interpolation, will produce a plot of the particle path:

fnplt(spapi(augknt(t,4,2),t,reshape(z,2,2*n)))

Vector-valued splines are also used in the approximation to gridded data, in any number of variables, using tensor-product splines. The same spline-construction commands are used, only the form of the input differs. For example, if x is an m-vector, y is an n-vector, and z is an array of size [m,n], then

cs = csapi({x,y},z);

describes a bicubic spline f satisfying 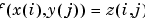 for 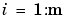 , 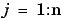. Such a multivariate spline can be vector-valued. For example,

x = 0:4; y=-2:2; s2 = 1/sqrt(2);
z(3,:,:) = [0 1 s2 0 -s2 -1 0].'*[1 1 1 1 1];
z(2,:,:) = [1 0 s2 1 s2 0 -1].'*[0 1 0 -1 0];
z(1,:,:) = [1 0 s2 1 s2 0 -1].'*[1 0 -1 0 1];
sph = csape({x,y},z,{'clamped','periodic'});
fnplt(sph), axis equal, axis off

gives a perfectly acceptable sphere. Its projection onto the (x,z)-plane is plotted by

fnplt(fncmb(sph,[1 0 0; 0 0 1]))

Both plots are shown below.

Figure 1-6: A Sphere Made by a 3-D-Valued Bivariate Tensor Product Spline

Figure 1-7: A Planar Projection of the Above Spline Sphere

Using the Spline Toolbox

Splines: An Overview