Signal Processing Toolbox

ss2zp

Convert state-space filter parameters to zero-pole-gain form.

Syntax

[z,p,k] = ss2zp(A,B,C,D,i)

Description

ss2zp converts a state-space representation of a given system to an equivalent zero-pole-gain representation. The zeros, poles, and gains of state-space systems represent the transfer function in factored form.

[z,p,k] = ss2zp(A,B,C,D,iu) calculates the transfer function in factored form

of the continuous-time system

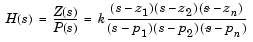
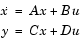
from the ith input (using the ith columns of B and D). The column vector p contains the pole locations of the denominator coefficients of the transfer function. The matrix z contains the numerator zeros in its columns, with as many columns as there are outputs y (rows in C). The column vector k contains the gains for each numerator transfer function.

ss2zp also works for discrete time systems. The input state-space system must be real.

The ss2zp function is part of the standard MATLAB language.

Example

Here are two ways of finding the zeros, poles, and gains of a discrete-time transfer function

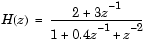
b = [2 3]; 
a = [1 0.4 1];
[b,a] = eqtflength(b,a);
[z,p,k] = tf2zp(b,a)
z =
    0.0000
   -1.5000
p =
    -0.2000 + 0.9798i
    -0.2000 - 0.9798i
k =
    2
[A,B,C,D] = tf2ss(b,a);
[z,p,k] = ss2zp(A,B,C,D,1)
z =
    0.0000
   -1.5000
p =
    -0.2000 + 0.9798i
    -0.2000 - 0.9798i
k =
    2

Algorithm

ss2zp finds the poles from the eigenvalues of the A array. The zeros are the finite solutions to a generalized eigenvalue problem.

z = eig([A B;C D], diag([ones(1,n) 0]);

In many situations this algorithm produces spurious large, but finite, zeros. ss2zp interprets these large zeros as infinite.

ss2zp finds the gains by solving for the first nonzero Markov parameters.

See Also

pzmap	Pole-zero map of LTI system (see the Control System Toolbox documentation).
sos2zp	Convert digital filter second-order section parameters to zero-pole-gain form.
ss2sos	Convert digital filter state-space parameters to second-order sections form.
ss2tf	Convert state-space filter parameters to transfer function form.
tf2zp	Convert transfer function filter parameters to zero-pole-gain form.
zp2ss	Convert zero-pole-gain filter parameters to state-space form.

References

[1] Laub, A.J., and B.C. Moore, "Calculation of Transmission Zeros Using QZ Techniques," Automatica 14 (1978), p. 557.

ss2tf

stmcb