

| Signal Processing Toolbox |   |
Change the cut-off frequency for a lowpass analog filter.
Syntax
[bt,at]=lp2lp(b,a,Wo) [At,Bt,Ct,Dt]=lp2lp(A,B,C,D,Wo)
Description
lp2lp transforms an analog lowpass filter prototype with a cutoff frequency of 1 rad/s into a lowpass filter with any specified cutoff frequency. The transformation is one step in the digital filter design process for the butter, cheby1, cheby2, and ellip functions.
The lp2lp function can perform the transformation on two different linear system representations: transfer function form and state-space form. In both cases, the input system must be an analog filter prototype.
Transfer Function Form (Polynomial)
[bt,at] transforms an analog lowpass filter prototype given by polynomial coefficients into a lowpass filter with cutoff frequency = lp2lp(b,a,Wo)
Wo. Row vectors b and a specify the coefficients of the numerator and denominator of the prototype in descending powers of s.
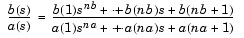
Scalar Wo specifies the cutoff frequency in units of radians/second. lp2lp returns the frequency transformed filter in row vectors bt and at.
State-Space Form
[At,Bt,Ct,Dt] converts the continuous-time state-space lowpass filter prototype in matrices = lp2lp(A,B,C,D,Wo)
A, B, C, D below
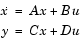
into a lowpass filter with cutoff frequency Wo. lp2lp returns the lowpass filter in matrices At, Bt, Ct, Dt.
Algorithm
lp2lp is a highly accurate state-space formulation of the classic analog filter frequency transformation. If a lowpass filter is to have cutoff frequency 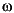 0, the standard s-domain transformation is
0, the standard s-domain transformation is
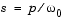
The state-space version of this transformation is
At=Wo*A; Bt=Wo*B; Ct=C; Dt=D;
See lp2bp for a derivation of the bandpass version of this transformation.
See Also
|
Bilinear transformation method for analog-to-digital filter conversion. |
|
Impulse invariance method for analog-to-digital filter conversion. |
|
Transform lowpass analog filters to bandpass. |
|
Transform lowpass analog filters to bandstop. |
|
Transform lowpass analog filters to highpass. |
 | lp2hp | lpc |  |