

| Signal Processing Toolbox |   |
Compute the Levinson-Durbin recursion.
Syntax
a = levinson(r,p)
Description
The Levinson-Durbin recursion is an algorithm for finding an all-pole IIR filter with a prescribed deterministic autocorrelation sequence. It has applications in filter design, coding, and spectral estimation. The filter that levinson produces is minimum phase.
a finds the coefficients of an = levinson(r,p)
pth-order autoregressive linear process which has r as its autocorrelation sequence. r is a real or complex deterministic autocorrelation sequence (a vector), and p is the order of denominator polynomial A(z); that is, a = [1 a(2) ... a(p+1)]. The filter coefficients are ordered in descending powers of z.
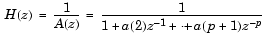
Algorithm
levinson solves the symmetric Toeplitz system of linear equations
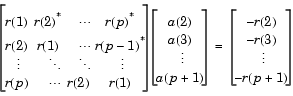
where r = [r(1) ... r(p+1)] is the input autocorrelation vector, and r(i)* denotes the complex conjugate of r(i). The algorithm requires O(p2) flops and is thus much more efficient than the MATLAB \ command for large p. However, the levinson function uses \ for low orders to provide the fastest possible execution.
See Also
lpc |
Compute linear prediction filter coefficients. |
prony |
Prony's method for time domain IIR filter design. |
rlevinson |
Compute the reverse Levinson-Durbin recursion. |
schurrc |
Compute reflection coefficients using Schur's algorithm. |
stmcb |
Compute a linear model using Steiglitz-McBride iteration. |
References
[1] Ljung, L., System Identification: Theory for the User, Prentice-Hall, 1987, pp. 278-280.
 | latcfilt | lp2bp |  |