

| Signal Processing Toolbox |   |
Compute the one-dimensional fast Fourier transform.
Syntax
y=fft(x) y=fft(x,n)
Description
fft computes the discrete Fourier transform of a vector or matrix. This function implements the transform given by
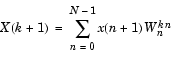
where WN = e-j(2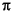 /N) and N
/N) and N = length(x). Note that the series is indexed as n + 1 and k + 1 instead of the usual n and k because MATLAB vectors run from 1 to N instead of from 0 to N-1.
y is the discrete Fourier transform of vector = fft(x)
x, computed with a fast Fourier transform (FFT) algorithm. If x is a matrix, y is the FFT of each column of the matrix.
y is the = fft(x,n)
n-point FFT. If the length of x is less than n, fft pads x with trailing zeros to length n. If the length of x is greater than n, fft truncates the sequence x. If x is an array, fft adjusts the length of the columns in the same manner.
The fft function is part of the standard MATLAB language.
Examples
A common use of the Fourier transform is to find the frequency components of a time-domain signal buried in noise. Consider data sampled at 1000 Hz. Form a signal consisting of 50 Hz and 120 Hz sinusoids and corrupt the signal with zero-mean random noise.
randn('state',0)
t = 0:0.001:0.6;
x = sin(2*pi*50*t) + sin(2*pi*120*t);
y = x + 2*randn(1,length(t));
plot(y(1:50))
It is difficult to identify the frequency components by studying the original signal. Convert to the frequency domain by taking the discrete Fourier transform of the noisy signal y using a 512-point fast Fourier transform (FFT).
Y = fft(y,512);
The power spectral density, a measurement of the energy at various frequencies, is
Pyy = Y.*conj(Y) / 512;
Graph the first 256 points (the other 256 points are symmetric) on a meaningful frequency axis.
f = 1000*(0:255)/512;
plot(f,Pyy(1:256))
See the pwelch function for details on estimating the spectral density.
Sometimes it is useful to normalize the output of fft so that a unit sinusoid in the time domain corresponds to unit amplitude in the frequency domain. To produce a normalized discrete-time Fourier transform in this manner, use
Pn = abs(fft(x))*2/length(x)
Algorithm
fft is a built-in MATLAB function. See the fft reference page in the MATLAB documentation for details about the algorithm.
See Also
|
Implement the discrete cosine transform (DCT). |
|
Compute the discrete Fourier transform matrix. |
|
Compute the two-dimensional fast Fourier transform. |
|
Rearrange the outputs of fft and fft2. |
|
Filter data. |
|
Compute the frequency response of digital filters. |
|
Compute the one-dimensional inverse fast Fourier transform. |
|
Estimate the power spectral density (PSD) of a signal using Welch's method. |
 | fdatool | fft2 |  |