

| Signal Processing Toolbox |   |
Syntax
xhat=cceps(x) [xhat,nd]=cceps(x) [xhat,nd,xhat1]=cceps(x) [...]=cceps(x,n)
Description
Cepstral analysis is a nonlinear signal processing technique that is applied most commonly in speech processing and homomorphic filtering [1].
xhat = cceps(x)
returns the complex cepstrum of the (assumed real) sequence x. The input is altered, by the application of a linear phase term, to have no phase discontinuity at ±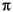 radians. That is, it is circularly shifted (after zero padding) by some samples, if necessary, to have zero phase at
radians. That is, it is circularly shifted (after zero padding) by some samples, if necessary, to have zero phase at 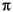 radians.
radians.
[xhat,nd] = cceps(x)
returns the number of samples nd of (circular) delay added to x prior to finding the complex cepstrum.
[xhat,nd,xhat1] = cceps(x)
returns a second complex cepstrum, computed using an alternate rooting algorithm, in xhat1. The alternate method ([1] p.795) is useful for short sequences that can be rooted and do not have zeros on the unit circle. For these signals, xhat1 can provide a verification of xhat.
[...] = cceps(x,n)
zero pads x to length n and returns the length n complex cepstrum of x.
Algorithm
cceps, in its basic form, is an M-file implementation of algorithm 7.1 in [2]. A lengthy Fortran program reduces to three lines of MATLAB code:
h=fft(x); logh=log(abs(h)) + sqrt(-1)*rcunwrap(angle(h)); y=real(ifft(logh));
rcunwrap is a special version of unwrap that subtracts a straight line from the phase.
See Also
|
Inverse complex cepstrum. |
|
Hilbert transform. |
|
Real cepstrum and minimum phase reconstruction. |
|
Unwrap phase angles. |
References
[1] Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1989.
[2] IEEE. Programs for Digital Signal Processing. IEEE Press. New York: John Wiley & Sons, 1979.
 | buttord | cell2sos |  |