

| Robust Control Toolbox |   |
System realization via Hankel singular value decomposition.
[a,b,c,d,totbnd,svh] = imp2ss(y) [a,b,c,d,totbnd,svh] = imp2ss(y,ts,nu,ny,tol) [ss,totbnd,svh] = imp2ss(imp) [ss,totbnd,svh] = imp2ss(imp,tol)
Description
The function imp2ss produces an approximate state-space realization of a given impulse response
imp=mksys(y,t,nu,ny,'imp');using the Hankel SVD method proposed by S. Kung [2]. A continuous-time realization is computed via the inverse Tustin transform (using
bilin) if t is positive; otherwise a discrete-time realization is returned. In the SISO case the variable y is the impulse response vector; in the MIMO case y is a N+1-column matrix containing N + 1 time samples of the matrix-valued impulse response H0, ..., HN of an nu-input, ny-output system stored row wise: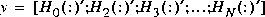 The variable tol bounds the H
The variable tol bounds the H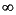 norm of the error between the approximate realization (a, b, c, d) and an exact realization of y; the order, say n, of the realization (a, b, c, d) is determined by the infinity norm error bound specified by the input variable tol. The inputs
norm of the error between the approximate realization (a, b, c, d) and an exact realization of y; the order, say n, of the realization (a, b, c, d) is determined by the infinity norm error bound specified by the input variable tol. The inputs ts, nu, ny, tol are optional; if not present they default to the values ts = 0, nu = 1, ny = (no. of rows of y)/nu, 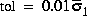 . The output
. The output 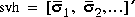 returns the singular values (arranged in descending order of magnitude) of the Hankel matrix:
returns the singular values (arranged in descending order of magnitude) of the Hankel matrix: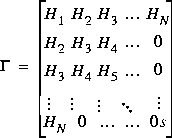 Denoting by GN a high-order exact realization of y, the low-order approximate model G enjoys the H
Denoting by GN a high-order exact realization of y, the low-order approximate model G enjoys the H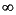 norm bound
norm bound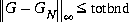 where
where 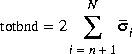
Algorithm
The realization (a, b, c, d) is computed using the Hankel SVD procedure proposed by Kung [2] as a method for approximately implementing the classical Hankel factorization realization algorithm. Kung's SVD realization procedure was subsequently shown to be equivalent to doing balanced truncation (balmr) on an exact state space realization of the finite impulse response {y(1),....y(N)} [3]. The infinity norm error bound for discrete balanced truncation was later derived by Al-Saggaf and Franklin [1]. The algorithm is as follows:
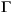 from the data y.
from the data y.
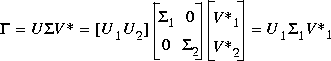
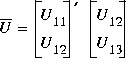
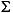 1 has dimension n x n and the entries of
1 has dimension n x n and the entries of 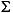 2 are nearly zero. U1 and V1 have ny and nu columns, respectively.
2 are nearly zero. U1 and V1 have ny and nu columns, respectively.
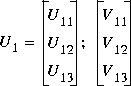
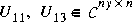 and
and 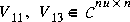 .
.
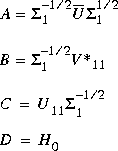
See Also
ohklmr, schmr, balmr, bstschmr
References
[1] U. M. Al-Saggaf and G. F. Franklin, "An Error Bound for a Discrete Reduced Order Model of a Linear Multivariable System," IEEE Trans. on Autom. Contr., AC-32, pp. 815-819, 1987.
 | hinfopt | interc |  |