hinfopt (Robust Control Toolbox)

H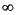 optimal control synthesis via 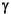-iteration.

[gamopt,acp,,dcp,acl,,dcl] = hinfopt(A,,D22) 
[gamopt,acp,,dcp,acl,,dcl] = hinfopt(A,,D22,gamind)
[gamopt,acp,,dcp,acl,,dcl] = hinfopt(A,,D22,gamind,aux) 
[gamopt,sscp,sscl] = hinfopt(tss) 
[gamopt,sscp,sscl] = hinfopt(tss,gamind) 
[gamopt,sscp,sscl] = hinfopt(tss,gamind,aux)

Description
hinfopt does H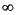 "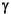-iteration" to compute the optimal H 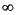controller using the loop-shifting two-Riccati formulae of hinf. The output gamopt is the optimal "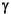" for which the cost function 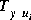can achieve under a preset tolerance

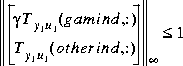
An optional input variable aux specifies the tolerance that stops the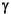

-iteration

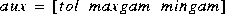where maxgam and mingam denotes a range for

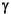-iteration to be carried out. The default value of aux is [0.01 1 0]. Another optional input variable gamind specifies the indices of the cost function output channels (i.e.,rows) to be scaled by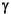

. Default for gamind is to scale all the output channels (gamind = 1: n).

Algorithm
A binary search algorithm is coded in hinfopt to achieve the required 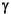-iteration. The iteration logic is based on the H 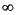existence tests performed inside hinf and recorded in the output variable hinfo of hinf. The search of optimal 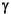stops whenever the 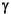relative error between two adjacent stable solutions is less than the tolerance specified. For most practical purposes, the tolerance can be set at 0.01 or 0.001.

Examples
Following are three simple problems solved via hinfopt with the SISO plant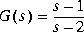

Problem 1: Mixed-Sensitivity

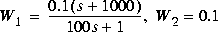, no W₃.

[ag,bg,cg,dg] = tf2ss([1 -1],[1 -2]); 
ssg = mksys(ag,bg,cg,dg); 
w1 = [0.1*[1 100];[100 1]]; w2 = [0.1;1]; w3 = []; 
[TSS] = augtf(ssg,w1,w2,w3); 
[gamopt,sscp,sscl] = hinfopt(TSS,[1:2],[0.001,1,0]);

In this case,

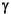opt = 1.5146.

Problem 2: W₁ is removed.

w1 = []; 
[TSS] = augtf(ssg,w1,w2,w3); 
[gamopt,sscp,sscl] = hinfopt(TSS,1,[0.001,1,0]);

In this case,

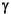opt = 2.5, F(s) = -4/3.

Problem 3: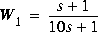

, W₂ is removed.

w1 = [1 1;10 1]; w2 = []; 
[TSS] = augtf(ssg,w1,w2,w3); 
[gamopt,sscp,sscl] = hinfopt(TSS,1,[0.001,1,0]);

For this problem,

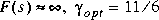These three very simple problems can be also solved analytically using the interpolation technique of [1], augmented in the case of problem 1 with the "two-block to one-block" embedding technique of [2]. The results of hinfopt match the exact solutions very well.

See Also
augss, augtf, hinf, linf

References
[1] G. Zames and B. A. Francis, "Feedback, Minimax Sensitivity, and Optimal Robustness," IEEE Trans. on Autom. Control, AC-28, 5, pp. 585-601, May 1983.

[2] M. Verma and E. A. Jonckheere, "L

-Compensation with Mixed Sensitivity as a Broadband Matching Problem," Systems and Control Letters, 4, pp. 125-129, May 1984.

hinf, dhinf, linf imp2ss