Distributed Parameter Line (Power System Blockset)

Implement an N-phase distributed parameter transmission line model with lumped losses.

Library

Elements

Description

The Distributed Parameter Line block implements an N-phase distributed parameter line model with lumped losses. The model is based on the Bergeron's travelling wave method used by the Electromagnetic Transient Program (EMTP)[1]. In this model, the lossless distributed LC line is characterized by two values (for a single phase line): the surge impedance 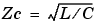and the phase velocity .

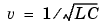The model uses the fact that the quantity e+Zi, where e is line voltage and i is line current, entering one end of the line must arrive unchanged at the other end after a transport delay of 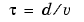, where d is the line length. By lumping R/4 at both ends of the line and R/2 in the middle and using the current injection method of the Power System Blockset, the following two-port model is derived:

where

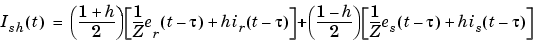
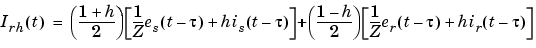
For multiphase line models, modal transformation is used to convert line quantities from phase values (line currents and voltages) into modal values independent of each other. The previous calculations are made in the modal domain before being converted back to phase values.

In comparison to the pi sections line model, the distributed line represents wave propagation phenomena and line end reflections with much better accuracy. See comparison between the two models in the Example section.

Dialog Box and Parameters

Number of phases N

Specifies the number of phases N of the model. The block icon dynamically changes according to the number of phases that you specify. When you apply the parameters or close the dialog box, the number of inputs and outputs is updated. The icon displays the individual conductors for N<=3. For N>3, only one conductor is displayed.

Frequency used for RLC specifications

Specifies the frequency used to compute the modal resistance R, inductance L, and capacitance C matrices of the line model.

Resistance per unit length

The resistance R per unit length, N-by-N matrix in ohms/km (

/km).

For a symmetrical line, you can either specify the N-by-N matrix or the sequence parameters: For a two-phase or three-phase continuously transposed line, you can enter the positive and zero-sequence resistances [R1 R0]. For a symmetrical six-phase line you can enter the sequence parameters plus the zero-sequence mutual resistance [R1 R0 R0m].

For unsymmetrical lines, you must specify the complete N-by-N resistance matrix.

Inductance per unit length

The inductance L per unit length, N-by-N matrix in henries/km (H/km).

For a symmetrical line, you can either specify the N-by-N matrix or the sequence parameters: For a two-phase or three-phase continuously transposed line, you can enter the positive and zero-sequence inductances [L1 L0]. For a symmetrical six-phase line you can enter the sequence parameters plus the zero-sequence mutual inductance [L1 L0 L0m].

For unsymmetrical lines, you must specify the complete N-by-N inductance matrix.

Capacitance per unit length

The Capacitance C per unit length, N-by-N matrix in farad/km (F/km).

For a symmetrical line, you can either specify the N-by-N matrix or the sequence parameters: For a two-phase or three-phase continuously transposed line, you can enter the positive and zero-sequence capacitances [C1 C0]. For a symmetrical six-phase line you can enter the sequence parameters plus the zero-sequence mutual capacitance [C1 C0 C0m].

For unsymmetrical lines, you must specify the complete N-by-N capacitance matrix.

Line length

The line length, in km.

Measurements

Select Phase-to-ground voltages to measure the sending end and receiving end voltages for each phase of the line model.

Place a Multimeter block in your model to display the selected measurements during the simulation. In the Available Measurement listbox of the Multimeter block, the measurement will be identified by a label followed by the block name:


Measurement	Label
Phase-to-ground voltages, sending end	`Us_ph1_gnd:, Us_ph2_gnd:, Us_ph3_gnd:, etc.`
Phase-to-ground voltages, receiving end	`Ur_ph1_gnd:, Ur_ph2_gnd:, Ur_ph3_gnd:, etc.`

Limitations

This model does not represent accurately the frequency dependence of R L C parameters of real power lines. Indeed, because of the skin effects in the conductors and ground, the R and L matrices exhibit strong frequency dependence, causing an attenuation of the high frequencies.

Example

A 200 km line is connected on a 1 kv, 60 Hz infinite source. The line is de-energized and then re-energized after 2 cycles. The simulation is performed simultaneously with the Distributed Parameter Line block and with the PI Section Line block. This circuit is available in the psbmonophaseline.mdl file.

The receiving end voltage obtained with the Distributed Parameter Line block is compared with the one obtained with the PI Section Line block (2 sections).

Open the powergui. In the Tools menu select Impedance vs Frequency Measurement. A new window appears, listing the two Impedance Measurement blocks connected to your circuit. Set the parameters of powergui to compute impedance in the 0:2000 Hz frequency range. Click on the Display button. The two impedances are displayed on the same graph.

Note that the distributed parameter line shows a succession of poles and zeros equally spaced, every 486 Hz. The first pole occurs a 243 Hz, corresponding to frequency f=1/(4*T) where:

T= travelling time= l *sqrt(L*C) =200*sqrt(2.137e-3*12.37e-9) = 1.028 ms

The pi section line only shows two poles because it consists of two pi sections. Impedance comparison shows that a two-section PI line gives a good approximation of the distributed line for the 0-350 Hz frequency range.

References

[1] Dommel, H, "Digital Computer Solution of Electromagnetic Transients in Single and Multiple Networks," IEEE Transactions on Power Apparatus and Systems", Vol PAS-88, No. 4, April 1969

See Also

PI Section Line, Multimeter

Discrete System Excitation System